
【題目】已知,四邊形ABCD是正方形,∠MAN=90°,將∠MAN繞頂點A旋轉,旋轉角為∠DAM(0°<∠DAM<45°),AM交CD于點E,∠MAN的平分線與CB交于點G
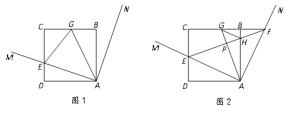
(1)證明:如圖1,連接GE.求證:GE=DE+BG;
(2)探究:如圖2,設AN交CB的延長線于點F,直線EF分別交AG,AB于點P,H.探究GH與AE的位置關系,并證明你的結論;
(3)應用:在圖2中,若正方形的邊長為6,BG=2,求GH的長.
【答案】(1)見解析;(2)GH∥AE,證明見解析;(3)![]()
【解析】
(1)延長CB交AN于點F,通過證△DAE≌△BAF和△EAG≌△FAG從而證得結論;(2)首先證明△PAH≌△PFG .則PH=PG ,從而∠PGH=45°. 又因為AP=EP,∠APE=90°. 所以∠PAE=45°.證得∠PGH=∠PAE,再根據平行線的判定得到GH∥AE;(3)設DE=![]() ,則CG=4,CE=6-
,則CG=4,CE=6-![]() ,GE=GF=2+
,GE=GF=2+![]() .在Rt△CEG中通過勾股定理求出x的值.再證△FBH∽△FCE,根據相似的性質即可求出BH的長,再在Rt△GBH中通過勾股定理求出GH的長.
.在Rt△CEG中通過勾股定理求出x的值.再證△FBH∽△FCE,根據相似的性質即可求出BH的長,再在Rt△GBH中通過勾股定理求出GH的長.
(1)證明:延長CB交AN于點F,
∵ABCD是正方形,∴AD=AB,∠DAB=∠D=∠ABF=90°.
∵∠MAN=90°,∴∠DAB=∠MAN.
∴∠DAB-∠EAB=∠MAN-∠EAB即:∠DAE=∠BAF.

∴△DAE≌△BAF.∴AE=AF.
又AG=AG,∠EAG=∠FAG.
∴△EAG≌△FAG .∴GE=GF.
而GF=BG+BF=BG+DE
∴GE=BG+DE.
(2)解: GH∥AE,證明如下:
∵AE=AF,AG平分∠EAF∴AG⊥EF,EP=FP.
∴∠APH=∠FPG=∠APE=90°,AP=![]() EF=EP=FP
EF=EP=FP
∴∠PFG+∠PGF=90又∵∠ABG=90°,∴∠PAH+∠PGF=90°.∴∠PAH=∠PFG.
∴△PAH≌△PFG .∴PH=PG .∴∠PGH=45°.
∵AP=EP,∠APE=90°. ∴∠PAE=45°.
∴∠PGH=∠PAE.∴GH∥AE.
(3)連接GE,由(1)知GE=GF,DE=BF.
設DE=![]() ,因為正方形邊長為6,BG=2,
,因為正方形邊長為6,BG=2,

∴CG=4,CE=6-![]() ,GE=GF=2+
,GE=GF=2+![]() .
.
在Rt△CEG中,CE2+CG2=GE2,
∴![]()
解得![]() ,即:DE=BF=3 .
,即:DE=BF=3 .
∴CE=6-3=3,CF=6+3=9 .
∵BH∥CE ∴△FBH∽△FCE ∴![]() .
.
∴BH=1
∵∠GBH=90° ∴GH=![]() .
.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:初中數學 來源: 題型:
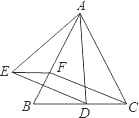
【題目】如圖,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC繞點A按順時針方向旋轉得到的.連接BE、CF相交于點D.
(1)求證:BE=CF.
(2)當四邊形ACDE為菱形時,求BD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC是等邊三角形,點D、F分別在線段BC、AB上,∠EFB=60°,DC=EF.
(1)求證:四邊形EFCD是平行四邊形;
(2)若BF=EF,求證:AE=AD.
查看答案和解析>>
科目:初中數學 來源: 題型:
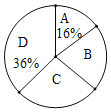
【題目】2020年4月是我國第32個愛國衛生月.某校九年級通過網課舉行了主題為“防疫有我,愛衛同行”的知識競賽活動.為了解全年級500名學生此次競賽成績(百分制)的情況,隨機抽取了部分參賽學生的成績,整理并繪制出如下不完整的統計表(表1)和統計圖(如圖).請根據圖表信息解答以下問題:
(1)本次調查一共隨機抽取了____個參賽學生的成績;
(2)表1中a=__;
(3)所抽取的參賽學生的成績的中位數落在的“組別”是__;
(4)統計圖中B組所占的百分比是_______;
(5)請你估計,該校九年級競賽成績達到80分以上(含80分)的學生人數.
表1 知識競賽成績分組統計表
組別 | 分數/分 | 頻數 |
A | 60≤x<70 | a |
B | 70≤x<80 | 10 |
C | 80≤x<90 | 14 |
D | 90≤x<100 | 18 |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,一元二次方程x2=﹣1沒有實數根,即不存在一個實數的平方等于﹣1.若我們規定一個新數“i”,使其滿足i2=﹣1(即方程x2=﹣1有一個根為i).并且進一步規定:一切實數可以與新數進行四則運算,且原有運算律和運算法則仍然成立,于是有i1=i,i2=﹣1,i3=i2×i=(﹣1)×i=﹣i,i4=(i2)2=(﹣1)2=1,從而對任意正整數n,我們可以得到i4n+1=i4n×i=(i4)n×i=i,i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+i4+…+i2012+i2013+…+i2019的值為( )
A.0B.1C.﹣1D.i
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】經銷商購進某種商品,當購進量在20千克~50千克之間(含20千克和50千克)時,每千克進價是5元;當購進量超過50千克時,每千克進價是4元.此種商品的日銷售量y(千克)受銷售價x(元/千克)的影響較大,該經銷商試銷一周后獲得如下數據:
x(元/千克) | 5 | 5.5 | 6 | 6.5 | 7 |
y(千克) | 90 | 75 | 60 | 45 | 30 |
解答下列問題:
(1)求出y關于x的一次函數表達式:
(2)若每天購進的商品能夠全部銷售完,且當日銷售價不變,日銷售利潤為w元,那么銷售價定為多少時,該經銷商銷售此種商品的當日利潤最大?最大利潤為多少元?此時購進量應為多少千克?(注:當日利潤=(銷售價-進貨價)×日銷售量).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小敏從![]() 地出發向
地出發向![]() 地行走,同時小聰從
地行走,同時小聰從![]() 地出發向
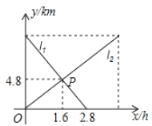
地出發向![]() 地行走,如圖,相交于點
地行走,如圖,相交于點![]() 的兩條線段
的兩條線段![]() 分別表示小敏、小聰離
分別表示小敏、小聰離![]() 地的距離
地的距離![]() 與已用時間
與已用時間![]() 之間的關 系,則
之間的關 系,則![]() _______時,小敏、小聰兩人相距
_______時,小敏、小聰兩人相距![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com