【題目】某校對七年級300名學生進行了教學質量監測（滿分100分），現從中隨機抽取部分學生的成績進行整理，并繪制成如圖不完整的統計表和統計圖：
注：60分以下為“不及格”，60～69分為“及格”，70～79分為“良好”，80分及以上為“優秀”
請根據以上信息回答下列問題：
（1）補全統計表和統計圖；
（2）若用扇形統計圖表示統計結果，則“良好”所對應扇形的圓心角為多少度？
（3）請估計該校七年級本次監測成績為70分及以上的學生共有多少人？
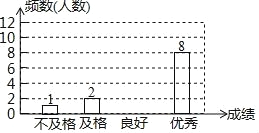
【答案】（1）9，0.40；（2）162°；（3）255．
【解析】
（1）首先根據不合格的人數及頻數求得總人數，然后減去其他各組的頻數即可求得良好組的頻數，用頻數除以總人數即可求得頻率；
（2）用良好的頻率乘以360°即可求得其表示的扇形的圓心角的度數；
（3）用總人數乘以70分以上的頻率即可求得人數．
解：（1）解：因為不及格的頻數為1，頻率為0.05，所以總人數為1÷0.05=20人，所以良好的頻數為20﹣1﹣2﹣8=9，優秀的頻率為8÷20=0.40．
故答案為：9，0.40；
統計圖補全為：
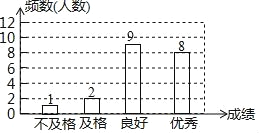
（2）0.45×360°=162°
答：“良好”所對應扇形的圓心角為162°；
（3）300×（0.45+0.40）=255．
答：估計該校本次監測成績70分及以上的學生總共約有255人．
故答案為：（1）9，0.40；（2）162°；（3）255．
科目：初中數學 來源： 題型：
【題目】甲、乙兩家草莓采摘園的草莓品質相同，銷售價格也相同．“五一期間”，兩家均推出了優惠方案，甲采摘園的優惠方案是：游客進園需購買50元的門票，采摘的草莓六折優惠；乙采摘園的優惠方案是：游客進園不需購買門票，采摘園的草莓超過一定數量后，超過部分打折優惠．優惠期間，設某游客的草莓采摘量為x（千克），在甲采摘園所需總費用為
（元），在乙采摘園所需總費用為
（元），圖中折線OAB表示
與x之間的函數關系．
（1）甲、乙兩采摘園優惠前的草莓銷售價格是每千克 元；
（2）求、
與x的函數表達式；
（3）在圖中畫出與x的函數圖象，并寫出選擇甲采摘園所需總費用較少時，草莓采摘量x的范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
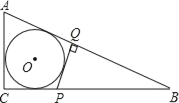
【題目】如圖，⊙O內切于Rt△ABC，點P、點Q分別在直角邊BC、斜邊AB上，PQ⊥AB，且PQ與⊙O相切，若AC＝2PQ，則tan∠B的值為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
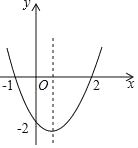
【題目】二次函數y＝ax2+bx+c的圖象如圖所示，以下結論：①abc＞0；②4ac＜b2；③2a+b＞0；④其頂點坐標為（
，﹣2）；⑤當x＜時，y隨x的增大而減小；⑥a+b+c＞0；⑦方程ax2+bx+c＝﹣4有實數解，正確的有（ ）
A. 3個 B. 4個 C. 5個 D. 6個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某人在山坡坡腳C處測得一座建筑物頂點A的仰角為63.4°，沿山坡向上走到P處再測得該建筑物頂點A的仰角為53°．已知BC=90米，且B、C、D在同一條直線上，山坡坡度i=5:12.
（1）求此人所在位置點P的鉛直高度．（結果精確到0.1米）
（2）求此人從所在位置點P走到建筑物底部B點的路程（結果精確到0.1米）
（測傾器的高度忽略不計，參考數據：tan53°≈
，tan63.5°≈2）
查看答案和解析>>
科目：初中數學 來源： 題型：
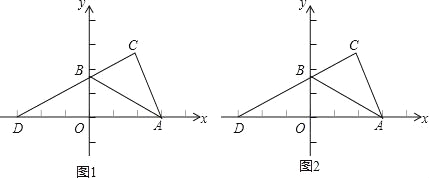
【題目】如圖，Rt△AOB在平面直角坐標系中，已知：B（0，
），點A在x軸的正半軸上，OA=3，∠BAD=30°，將△AOB沿AB翻折，點O到點C的位置，連接CB并延長交x軸于點D．
（1）求點D的坐標；
（2）動點P從點D出發，以每秒2個單位的速度沿x軸的正方向運動，當△PAB為直角三角形時，求t的值；
（3）在（2）的條件下，當△PAB為以∠PBA為直角的直角三角形時，在y軸上是否存在一點Q使△PBQ為等腰三角形？如果存在，請直接寫出Q點的坐標；如果不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
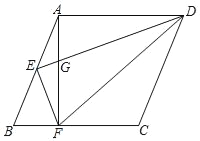
【題目】如圖，已知菱形ABCD，點E是AB的中點，AF⊥BC于點F，聯結EF、ED、DF，DE交AF于點G，且AE2＝EGED．
(1)求證：DE⊥EF；
(2)求證：BC2＝2DFBF．
查看答案和解析>>
科目：初中數學 來源： 題型：
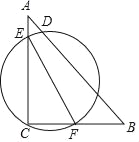
【題目】如圖，△ABC中，∠C＝90°，AC＝8，BC＝6，E，F分別在邊AC，BC，若以EF為直徑作圓經過AB上某點D，則EF長的取值范圍為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
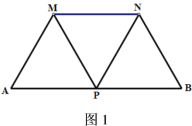
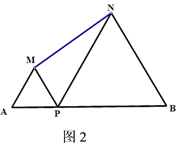
【題目】如圖1所示，點P是線段AB的中點，且AB=12，現分別以AP，BP為邊，在AB的同側作等邊△MAP和△NBP，連結MN。
(1)請只用不含刻度的直尺在圖1中找到△MNP外接圓的圓心O，并保留作圖痕跡；
(2)若將“點P是線段AB的中點”改成“點P是線段AB上異于端點的任意一點”，其余條件不變(如圖2)，請用文字寫出△MNP外接圓圓心O的位置，并求出該圓半徑的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com