
【題目】在一次數學社團活動中,指導老師給同學們提出了以下問題:
問題:有67張卡片疊在一起,按從上而下的順序先把第一張拿走,把第二張放到底層,然后把第三張拿走,再把第四張放到底層,如此進行下去,直至只剩最后一張卡片.問僅剩的這張卡片是原來的第幾張卡片?
由于卡片數量較多,指導老師建議同學們先對較少的張數進行嘗試,以便熟悉游戲規則并發現一些規律!
(1)請你試著在草稿紙上進行試驗,將試驗結果填寫在下表中:
試驗的卡片數量 (張) | 2 | 4 | 8 | 9 | 10 | 11 |
剩下最后一張卡片是 原來卡片的第幾張 |
(2)根據試驗結果的規律,回答最初的67張卡片情形,請你給出答案并簡要說明理由.
【答案】(1)表格依次填2、4、8、2、4、6;(2)最初是67張卡片,最后剩下的是原來的第6張,理由見解析
【解析】
(1)根據題意依次確定每次拿走的是第幾張,即可得到剩下的一張是原來的第幾張;
(2)根據前面的結果可以得到最初64張卡片時最后剩下的是原來的第64張,依此推理得到最初67張卡片時的最后一張是原來的第幾張即可得到答案.
(1)根據題意:
當卡片是2張時,第一次拿走第1張,剩下的是第2張,
當卡片是4張時,第一次拿走第1張和第3張,第二次拿走第2張,剩下的是第4張,
當卡片是8張時,第一次拿走第1張、第3張、第5張、第7張,第二次拿走第2張、第6張,第三次拿走第4張,剩下的是第8張,
當卡片是9張時,第一次拿走第1張、第3張、第5張、第7張、第9張,第二次拿走第4張、第8張,第三次拿走第6張,剩下的是第2張,
當卡片是10張時,第一次拿走第1張、第3張、第5張、第7張、第9張,第二次拿走第2張、第6張、第10張,第三次拿走第8張,剩下的是第4張,
當卡片是11張時,第一次拿走第1張、第3張、第5張、第7張、第9張、第11張,第二次拿走第4張、第8張,第三次拿走第2張、第10張,剩下的是第6張,
故答案為:2、4、8、2、4、6;
(2)根據實驗結果進行規律總結,直角判斷若最初64張卡片,最后剩下的是第64張,最初是67張卡片,最后剩下的是原來的第6張,理由如下:
最初是67張卡片時,第一次拿走第1張、第3張、第5張、第7張、第9張、第11張、![]() 、第67張,
、第67張,
第二次拿走第4張、第8張、第12張、![]() 、第64張,
、第64張,
第三次拿走第2張、第10張、第18張、第26張、第34張、第42張、第50張、第58張、第66張,
第四次拿走第14張、第22張、第30張、第38張、第46張、第54張、第62張,
∴最后剩下的是原來的第6張.


科目:初中數學 來源: 題型:
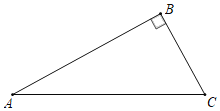
【題目】已知,如圖,在直角三角形ABC中,∠ABC=90°,AC=10,BC=6,AB=8.P是線段AC上的一個動點,當點P從點C向點A運動時,運動到點A停止,設PC=x,△ABP的面積為y.求y與x之間的關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】生活中,有人喜歡把傳送的便條折成“ ”形狀,折疊過程按圖
”形狀,折疊過程按圖![]() 的順序進行(其中陰影部分表示紙條的反面):
的順序進行(其中陰影部分表示紙條的反面):

如果由信紙折成的長方形紙條(圖①)長![]() 厘米,分別回答下列問題:
厘米,分別回答下列問題:
(1)如圖①、圖②,如果長方形紙條的寬為![]() 厘米,并且開始折疊時
厘米,并且開始折疊時![]() 厘米,那么在圖②中,
厘米,那么在圖②中,![]() ____厘米.
____厘米.
(2)如圖②,如果長方形紙條的寬為![]() 厘米,現在不但要折成圖②的形狀,還希望紙條兩端超出點
厘米,現在不但要折成圖②的形狀,還希望紙條兩端超出點![]() 的部分
的部分![]() 和
和![]() 相等,使圖②. 是軸對稱圖形,
相等,使圖②. 是軸對稱圖形,![]() ______厘米.
______厘米.
(3)如圖④,如果長方形紙條的寬為![]() 厘米,希望紙條兩端超出點
厘米,希望紙條兩端超出點![]() 的部分
的部分![]() 和
和![]() 相等,即最終圖形是軸對稱圖形,試求在開始折疊時起點
相等,即最終圖形是軸對稱圖形,試求在開始折疊時起點![]() 與點
與點![]() 的距離(結果用
的距離(結果用![]() 表示) .
表示) .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數![]() ,其中
,其中![]() .
.
(1)若點![]() 在y1的圖象上.求a的值:
在y1的圖象上.求a的值:
(2)當![]() 時.若函數有最大值2.求y1的函數表達式;
時.若函數有最大值2.求y1的函數表達式;
(3)對于一次函數![]() ,其中
,其中![]() ,若對- -切實數x,
,若對- -切實數x,![]() 都成立,求a,m需滿足的數量關系及 a的取值范圍.
都成立,求a,m需滿足的數量關系及 a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“囧”(jiǒng)是一個風靡網絡的流行詞,像一個人臉郁悶的神情.如圖所示,一張邊長為![]() 的正方形的紙片,剪去兩個一樣的小直角三角形和一個長方形得到一個“囧”字圖案(陰影部分).設剪去的小長方形長和寬分別為
的正方形的紙片,剪去兩個一樣的小直角三角形和一個長方形得到一個“囧”字圖案(陰影部分).設剪去的小長方形長和寬分別為![]() 、
、![]() ,剪去的兩個小直角三角形的兩直角邊長也分別為
,剪去的兩個小直角三角形的兩直角邊長也分別為![]() 、
、![]() .
.

(1)用含有![]() 、
、![]() 的式子表示圖中“囧”(陰影部分)的面積;
的式子表示圖中“囧”(陰影部分)的面積;
(2)當![]() ,
,![]() 時,求此時“囧”(陰影部分)的面積.
時,求此時“囧”(陰影部分)的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
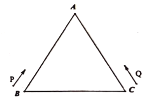
【題目】如圖,等邊三角形![]() 的周長為
的周長為![]() ,
,![]() ,
,![]() 兩點分別從
兩點分別從![]() ,
,![]() 兩點同時出發,點
兩點同時出發,點![]() 以
以![]() 的速度按順時針方向在三角形的邊上運動,點
的速度按順時針方向在三角形的邊上運動,點![]() 以
以![]() 的速度按逆時針方向在三角形的邊上運動.設
的速度按逆時針方向在三角形的邊上運動.設![]() ,
,![]() 兩點第一次在三角形
兩點第一次在三角形![]() 的頂點處相遇的時間為
的頂點處相遇的時間為![]() ,第二次在三角形
,第二次在三角形![]() 頂點處相遇的時間為
頂點處相遇的時間為![]() ,則
,則![]() _______.
_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有A、B兩組卡片共5張,A組的三張分別寫有數字2,4,6,B組的兩張分別寫有3,5.它們除了數字外沒有任何區別,
(1)隨機從A組抽取一張,求抽到數字為2的概率;
(2)隨機地分別從A組、B組各抽取一張,請你用列表或畫樹狀圖的方法表示所有等可能的結果.現制定這樣一個游戲規則:若選出的兩數之積為3的倍數,則甲獲勝;否則乙獲勝.請問這樣的游戲規則對甲乙雙方公平嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,甲、乙兩動點分別從正方形![]() 的頂點
的頂點![]() 同時沿正方形的邊開始移動,甲按順時針方向環行,乙按逆時針方向環行,若乙的速度是甲的3倍,那么它們第1次相遇在邊
同時沿正方形的邊開始移動,甲按順時針方向環行,乙按逆時針方向環行,若乙的速度是甲的3倍,那么它們第1次相遇在邊![]() 上.
上.

(1)它們第2次相遇在邊__________上;
(2)它們第2019次相遇在邊__________上.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com