
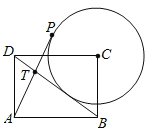
【題目】如圖,在矩形ABCD中,AB=3,![]() ,以點C為圓心作⊙O與直線BD相切,點P是⊙O上的一個動點,連接AP交BD于點T,則
,以點C為圓心作⊙O與直線BD相切,點P是⊙O上的一個動點,連接AP交BD于點T,則![]() 的最大值是( )
的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
【答案】D
【解析】
如圖,過點A作AG⊥BD于G點,利用矩形的性質結合勾股定理求出BD,由此提高等面積法求得![]() ,從而得分析出圓的半徑為
,從而得分析出圓的半徑為![]() ,緊接著過點P作PE⊥BD于點E,提高證明
,緊接著過點P作PE⊥BD于點E,提高證明![]() 利用相似三角形性質得出
利用相似三角形性質得出![]() ,據此根據題意分析出要使
,據此根據題意分析出要使![]() 最大,則
最大,則![]() 最大,即PE最大,最后進一步分析求解即可.
最大,即PE最大,最后進一步分析求解即可.
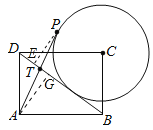
如圖,過點A作AG⊥BD于G點,
∵∠BAD=90°,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴點C到BD的距離為![]() ,
,
∵BD是圓的切線,
∴圓的半徑為![]() ,
,
過點P作PE⊥BD于點E,
∴∠AGT=∠PET,
∵∠ATG=∠PTE,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
要使![]() 最大,則
最大,則![]() 最大,即PE最大,
最大,即PE最大,
∵點P是圓上動點,BD是圓的切線,
∴PE最大為圓的直徑,
即PE最大值為:3,
∴![]() 最大值為
最大值為![]() ,
,
故選:D.


科目:初中數學 來源: 題型:
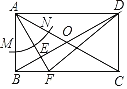
【題目】如圖,在矩形ABCD中,對角線AC與BD交于點O,已知AB=OA,按以下步驟作圖:①以點A為圓心,以任意長為半徑畫弧交AB于M,交AC于點N;②分別以點M,N為圓心,以大于![]() MN為半徑畫弧,兩弧相交于點E;③作射線AE交BC于點F,連接DF.若AB=
MN為半徑畫弧,兩弧相交于點E;③作射線AE交BC于點F,連接DF.若AB=![]() ,則線段DF的長為_____.
,則線段DF的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,一根木棒AB,斜靠在與地面OM垂直的墻壁ON上,當木棒A端沿NO向下滑動時,同時B端沿射線OM向右滑動,實踐發現木棒的中點P運動的路徑是一個優美的幾何圖形,我們把這樣的點叫優美點.如果木棒AB長為4,與地面的傾斜角∠ABO=60°.
(1)當木棒A端沿NO向下滑動到點O時,同時B端沿射線OM向右滑動到B′時,木棒的中點P所經過的路徑長為多少?
(2)若點P為OB上由點O向點B運動的一運動點,連接AP.
①如圖2,設AP的中點為G,問點G是不是優美點,如是,請求出點P運動過程中G所經過的路徑長.
②如圖3,過點B作BR⊥AP,垂足為點R.點P運動過程中,點R是不是優美點,如是,請求出點R所經過的路徑長.
(3)如圖4,若點P以每秒1個單位長度由點B向點O運動,同時點Q以每秒![]() 個單位長度的速度由點A向點O運動,連接PQ,S為PQ的中點,則在PQ的運動過程中,點S經過的路徑長為多少?(直接寫結果)
個單位長度的速度由點A向點O運動,連接PQ,S為PQ的中點,則在PQ的運動過程中,點S經過的路徑長為多少?(直接寫結果)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
一般地,如果一個數列從第![]() 項起,每一項與它的前一項的差等于同一個常數,那么這個數列就叫等差數列,這個常數叫做等差數列的公差,它通常用字母
項起,每一項與它的前一項的差等于同一個常數,那么這個數列就叫等差數列,這個常數叫做等差數列的公差,它通常用字母![]() 表示,我們可以用公式
表示,我們可以用公式![]() 來計算等差數列的和.(公式中的n表示數的個數,a表示第一個數的值,)
來計算等差數列的和.(公式中的n表示數的個數,a表示第一個數的值,)
例如:3+5+7+9+11+13+15+17+19+21=10×3+![]() ×2=120.
×2=120.
用上面的知識解決下列問題.
(1)計算:2+8+14+20+26+32+38+44+50+56+62+68+74+80+86+92+98+104+110+116
(2)某縣決定對坡荒地進行退耕還林.從2009年起在坡荒地上植樹造林,以后每年植樹后坡荒地的實際面積按一定規律減少,下表為2009、2010、2011、2012四年的坡荒地面積的統計數據.問到哪一年,可以將全縣所有坡荒地全部種上樹木.
2009年 | 2010年 | 2011年 | 2012年 | |
植樹后坡荒地的實際面積(公頃) | 25 200 | 24 000 | 22 400 | 20400 |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了加強學生課外閱讀,開闊視野,某校開展了“書香校園,誦讀經典”活動,學校隨機抽查了部分學生,對他們每天的課外閱讀時間進行調查,并將調查統計的結果分為四類:每天誦讀時間![]() 分鐘的學生記為
分鐘的學生記為![]() 類,20分鐘
類,20分鐘![]() 分鐘記為
分鐘記為![]() 類,40分鐘
類,40分鐘![]() 分鐘記為
分鐘記為![]() 類,
類,![]() 分鐘記為
分鐘記為![]() 類,收集的數據繪制如下兩幅不完整的統計圖.請根據圖中提供的信息,解答下列問題:
類,收集的數據繪制如下兩幅不完整的統計圖.請根據圖中提供的信息,解答下列問題:
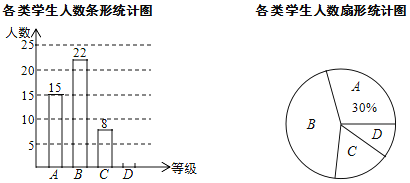
(1)這次共抽取了__________名學生進行調查統計,扇形統計圖中![]() 類所對應的扇形圓心角大小為___________;
類所對應的扇形圓心角大小為___________;
(2)將條形統計圖補充完整;
(3)如果該校共有2000名學生,請你估計該校![]() 類學生約有多少人?
類學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中正確的是( )
A. “打開電視,正在播放新聞節目”是必然事件
B. “拋一枚硬幣,正面進上的概率為![]() ”表示每拋兩次就有一次正面朝上
”表示每拋兩次就有一次正面朝上
C. “拋一枚均勻的正方體骰子,朝上的點數是6的概率為![]() ”表示隨著拋擲次數的增加,“拋出朝上的點數是6”這一事件發生的頻率穩定在
”表示隨著拋擲次數的增加,“拋出朝上的點數是6”這一事件發生的頻率穩定在![]() 附近
附近
D. 為了解某種節能燈的使用壽命,選擇全面調查
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx﹣3a經過點A(﹣1,0)、C(0,3),與x軸交于另一點B,拋物線的頂點為D.

(1)求此二次函數解析式;
(2)連接DC、BC、DB,求證:△BCD是直角三角形;
(3)在對稱軸右側的拋物線上是否存在點P,使得△PDC為等腰三角形?若存在,求出符合條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在矩形ABCD中,P為CD邊上一點(DP<CP),∠APB=90°.將△ADP沿AP翻折得到△AD′P,PD′的延長線交邊AB于點M,過點B作BN∥MP交DC于點N.
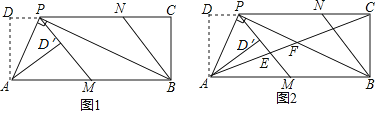
(1)求證:AD2=DPPC;
(2)請判斷四邊形PMBN的形狀,并說明理由;
(3)如圖2,連接AC,分別交PM,PB于點E,F.若![]() =
=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com