
【題目】如圖![]() 是一個矩形桌子,一小球從
是一個矩形桌子,一小球從![]() 撞擊到
撞擊到![]() ,反射到
,反射到![]() ,又從
,又從![]() 反射到
反射到![]() ,從
,從![]() 反射回原處
反射回原處![]() ,入射角與反射角相等(例如
,入射角與反射角相等(例如![]() 等),已知
等),已知![]() ,
,![]() ,
,![]() .則小球所走的路徑的長為__________.
.則小球所走的路徑的長為__________.
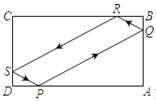
【答案】30
【解析】
求出四邊形SPQR是平行四邊形,推出SR=PQ,PS=QR,證三角形全等得出BR=DP,BQ=DS,根據相似求出DS,根據勾股定理求出即RS,RQ,PQ,SP即可.
∵入射角與反射角相等,
∴∠BQR=∠AQP,∠APQ=∠SPD,∠CSR=∠DSP,∠CRS=∠BRQ,
∵四邊形ABCD是矩形,
∴∠A=∠B=∠C=∠D=90![]() ,
,
∴∠DPS+∠DSP=90![]() ,∠AQP+∠APQ=90
,∠AQP+∠APQ=90![]() ,
,
∴∠DSP=∠AQP=∠CSR=∠BQR,
∴∠RSP=∠RQP,
同理∠SRQ=∠SPQ,
∴四邊形SPQR是平行四邊形,
∴SR=PQ,PS=QR,
在△DSP和△BQR中
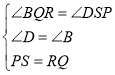
∴△DSP≌△BQR,
∴BR=DP=4,BQ=DS,
∵四邊形ABCD是矩形,
∴AB=CD=9,BC=AD=12,
∴AQ=9DS,AP=124=8,
∵∠SPD=∠APQ,
∴△SDP∽△QAP,
∴![]()
∴![]() ,
,
DS=3,
在Rt△DSP中,由勾股定理得:PS=QR=![]() ,
,
∵![]()
∴PQ=RS=10,
∴QP+PS+SR+QR=2×5+2×10=30,
故答案為:30.


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:
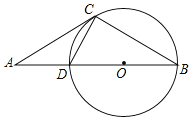
【題目】如圖,點A是⊙O直徑BD延長線上的一點,AC是⊙O的切線,C為切點.AD=CD,
(1)求證:AC=BC;
(2)若⊙O的半徑為1,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠ABC=70°,以B為圓心,任意長為半徑畫弧交AB,BC于點E,F,再分別以點E,F為圓心、以大于![]() EF長為半徑畫弧,兩弧交于點P,作射線BP交AC于點D,則∠BDC為( )度.
EF長為半徑畫弧,兩弧交于點P,作射線BP交AC于點D,則∠BDC為( )度.
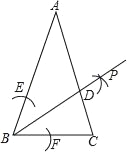
A. 65 B. 75 C. 80 D. 85
查看答案和解析>>
科目:初中數學 來源: 題型:
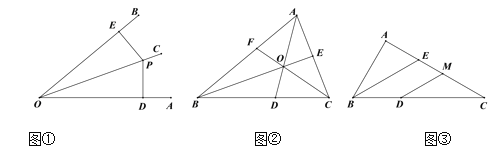
【題目】教材呈現:如圖是華師版八年級上冊數學教材第96頁的部分內容.

(1)定理證明:請根據教材中的分析,結合圖①,寫出“角平分線的性質定理”完整的證明過程.
(2)定理應用:如圖②,在△ABC中,AD、BE分別是∠BAC、∠ABC的角平分線,AD、BE的交點為O,連結CO交AB于點F,求證:∠ACF=∠BCF.
(3)如圖③,在(2)的條件下,若BE=CE,∠C=30°,△ABD沿AD翻折使點B落在邊AC上的點M處,連結DM,其中AB=![]() ,則S△DCM= .
,則S△DCM= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2﹣2ax+c與x軸交于A,B兩點(A在B左側),與y軸正半軸交于點C,且滿足:(1)一元二次方程ax2﹣2ax+c=0的一個解是﹣1;(2)拋物線的頂點在直線y=2x上.
問:(1)直接寫出A、B兩點的坐標.
(2)求此拋物線的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
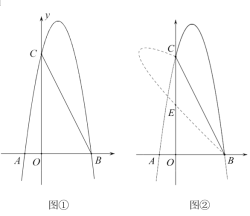
【題目】如圖①,拋物線![]() 過
過![]() 、
、![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() ,連接
,連接![]() .
.
(1)求該拋物線的表達式和對稱軸;
(2)點![]() 是拋物線對稱軸上一動點,當
是拋物線對稱軸上一動點,當![]() 是以
是以![]() 為直角邊的直角三角形時,求所有符合條件的點
為直角邊的直角三角形時,求所有符合條件的點![]() 的坐標;
的坐標;
(3)如圖②,將拋物線在![]() 上方的圖象沿
上方的圖象沿![]() 折疊后與
折疊后與![]() 軸交與點
軸交與點![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明家所在居民樓的對面有一座大廈AB,高為74米,為測量居民樓與大廈之間的距離,小明從自己家的窗戶C處測得大廈頂部A的仰角為37°,大廈底部B的俯角為48°.
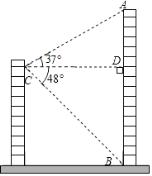
(1)求∠ACB的度數;
(2)求小明家所在居民樓與大廈之間的距離.(參考數據:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin48°≈
,sin48°≈![]() ,cos48°≈
,cos48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
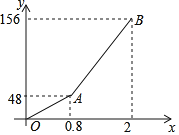
【題目】元旦期間,小黃自駕游去了離家156千米的黃石礦博園,右圖是小黃離家的距離y(千米)與汽車行駛時間x(小時)之間的函數圖象.
(1)求小黃出發0.5小時時,離家的距離;
(2)求出AB段的圖象的函數解析式;
(3)小黃出發1.5小時時,離目的地還有多少千米?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com