
【題目】△ABC在平面直角坐標系中的位置如圖所示,其中每個小正方形的邊長為1個單位長度.

(1)畫出△ABC關于x軸對稱的圖形△A1B1C1,
(2)寫出點A的對應點A1的坐標;
(3)將△ABC的橫、縱坐標分別乘以-1,畫出對應的圖形△A2B2C2;若P(a,b)為△ABC邊上一點,則在△A2B2C2中,點P對應的點Q的坐標為 .
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線y=ax2+4x+c(a≠0)經過點A(3,﹣4)和B(0,2).
(1)求拋物線的表達式和頂點坐標;
(2)將拋物線在A、B之間的部分記為圖象M(含A、B兩點).將圖象M沿直線x=3翻折,得到圖象N.若過點C(9,4)的直線y=kx+b與圖象M、圖象N都相交,且只有兩個交點,求b的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線![]() 與
與![]() 交于A,B兩點,且點A的橫坐標為4,過原點O的另一條直線l交雙曲線
交于A,B兩點,且點A的橫坐標為4,過原點O的另一條直線l交雙曲線![]() 于P,Q兩點(點P在第一象限),由點A,B,P,Q為頂點組成的四邊形面積為24,則點P的坐標為_________.
于P,Q兩點(點P在第一象限),由點A,B,P,Q為頂點組成的四邊形面積為24,則點P的坐標為_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下題及證明過程:已知:如圖,D是△ABC中BC邊上一點,E是AD上一點,EB=EC,∠ABE=∠ACE,求證:∠BAE=∠CAE.
證明:在△AEB和△AEC中,
∵EB=EC,∠ABE=∠ACE,AE=AE,
∴△AEB≌△AEC…第一步
∴∠BAE=∠CAE…第二步
問上面證明過程是否正確?若正確,請寫出每一步推理的依據;若不正確,請指出錯在哪一步,并寫出你認為正確的證明過程.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+c(a≠0)與x軸相交于A,B兩點,與y軸相交于點C,直線y=kx+n(k≠0)經過B,C兩點,已知A(1,0),C(0,3),且BC=5.
(1)分別求直線BC和拋物線的解析式(關系式);
(2)在拋物線的對稱軸上是否存在點P,使得以B,C,P三點為頂點的三角形是直角三角形?若存在,請求出點P的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某農場要建一個飼養場(矩形ABCD)兩面靠現有墻(AD位置的墻最大可用長度為27米,AB位置的墻最大可用長度為15米),另兩邊用木欄圍成,中間也用木欄隔開,分成兩個場地及一處通道,并在如圖所示的三處各留1米寬的門(不用木欄).建成后木欄總長45米.設飼養場(矩形ABCD)的一邊AB長為x米.

(1)飼養場另一邊BC=____米(用含x的代數式表示).
(2)若飼養場的面積為180平方米,求x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某加工企業生產并銷售某種農產品,假設銷售量與加工產量相等.已知每千克生產成本y1(單位:元)與產量x(單位:kg)之間滿足表達式y1=![]() 下圖中線段AB表示每千克銷售價格y2(單位:元)與產量x(單位:kg)之間的函數表達式.
下圖中線段AB表示每千克銷售價格y2(單位:元)與產量x(單位:kg)之間的函數表達式.
(1)試確定每千克銷售價格y2與產量x之間的函數表達式,并寫出自變量的取值范圍;
(2)若用w(單位:元)表示銷售該農產品的利潤,試確定w與產量x之間的函數表達式;
(3)求銷售量為70 kg時,銷售該農產品是賺錢,還是虧本?賺錢或虧本了多少元?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點A(1,0),B(1﹣a,0),C(1+a,0)(a>0),點P在以D(4,4)為圓心,1為半徑的圓上運動,且始終滿足∠BPC=90°,則a的最大值是______.
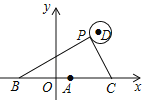
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是用4個全等的直角三角形于1個小正方形鑲嵌而成的正方形圖案,已知大正方形面積為49,小正方形面積為4,若用x、y表示三角形的兩條直角邊(x>y),下列四個說法:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 。其中說法正確的是( )
。其中說法正確的是( )

A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com