
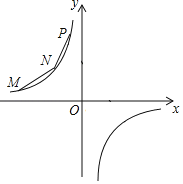
【題目】如圖所示,M、N、P在第二象限,橫坐標分別是﹣4、﹣2、﹣1,雙曲線y=![]() 過M、N、P三點,且MN=NP.
過M、N、P三點,且MN=NP.
(1)求雙曲線的解析式;
(2)過P點的直線l交x軸于A,交y軸于B,且PA=4AB,且交y=![]() 于另一點Q,求Q點坐標;
于另一點Q,求Q點坐標;
(3)以PN為邊(順時針方向)作正方形PNEF,平移正方形使N落在x軸上,點P、E對應的點P′、E'正好落在反比例函數y=![]() 上,求F對應點F′的坐標.
上,求F對應點F′的坐標.
【答案】(1)雙曲線的解析式為y=﹣![]() ;(2)Q(
;(2)Q(![]() ,﹣5);(3)點F′的坐標為(﹣5,3).
,﹣5);(3)點F′的坐標為(﹣5,3).
【解析】
(1)先表示出點M,N,P的坐標,進而得出MN2,NP2,建立方程求解,即可得出結論;
(2)分點A在x軸的正半軸或負半軸上,判斷出△AOB∽∠PQB,得出比例式,即可得出結論;
(3)先確定出點E,F坐標,設出點N'的坐標,進而得出點E',F',P'的坐標,即可得出結論.
(1)∵雙曲線y=![]() 過M、N、P三點,
過M、N、P三點,
∴M(﹣4,﹣![]() ),N(﹣2,﹣
),N(﹣2,﹣![]() ),P(﹣1,﹣k),
),P(﹣1,﹣k),
∴MN2=[(﹣4﹣(﹣2)]2+[(﹣![]() )﹣(﹣
)﹣(﹣![]() )]2=4+
)]2=4+![]() ,NP2=1+
,NP2=1+![]() ,
,
∵MN=NP,
∴MN2=NP2,
∴4+![]() =1+
=1+![]() ,
,
∴k=﹣4或k=4(由于點P在第二象限,不符合題意,舍去),
∴雙曲線的解析式為y=﹣![]() ;
;
(2)由(1)知,雙曲線的解析式為y=﹣![]() ①,
①,
由(1)知,k=﹣4,
∴P(﹣1,4),
如圖1,過點P作PQ⊥y軸于Q,則PQ=1,
Ⅰ、當點A在x軸正半軸時,
∵PA=4AB,
∴PB=3AB,
∵PQ⊥y軸,OA⊥y軸,
∴OA∥PQ,
∴△AOB∽∠PQB,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴OA=![]() ,
,
∴A(![]() ,0),
,0),
∵P(﹣1,4),
∴直線PA的解析式為y=﹣3x+1②,
聯立①②解得,![]() 或
或 ,
,
∴Q(![]() ,﹣3),
,﹣3),
Ⅱ、當點A在x軸負半軸上,
∵PA'=A'B',
∴PB'=5A'B',
同(Ⅰ)的方法得,△A'OB'∽△PQB',
∴![]() ,
,
∴![]() ,
,
∴OA'=![]() ,
,
∴A'(﹣![]() ,0),
,0),
∴直線PA'的解析式為y=﹣5x﹣1③,
聯立①③解得,![]() 或
或 ,
,
∴Q(![]() ,﹣5);
,﹣5);
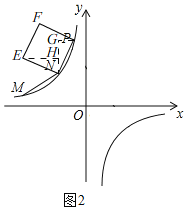
(3)如圖2,由(1)知,k=﹣4,
∴P(﹣1,4),N(﹣2,2),
∵四邊形PNEF是正方形,
∴EN=PN,∠PNE=90°,
過點N作y軸的平行線交過點P作x軸的平行線于G,過點E作EH⊥NG于H,
∴∠EHN=∠NGP=90°,
∴∠HEN+∠ENH=90°,∠ENH+∠PNG=90°,
∴∠HEN=∠GNP,
∴△EHN≌△NGP(AAS),
∴NH=PG=|﹣2﹣(﹣1)|=1,EH=NG=|4﹣2|=2,
∴E(﹣4,3),
同理:F(﹣3,5),
記點N平移到x軸的N'位置,設N'(m,0),
∵N(﹣1,4),
∴點N向左平移(﹣2﹣m)個單位,再向下平移2個單位,
∴點P,E,F也向左平移(﹣2﹣m)個單位,再向下平移2個單位,得到點P'(m+1,2),E'(m﹣2,1),F'(m﹣1,3),
∴點P′、E'正好落在反比例函數y=![]() 上,
上,
∴b=2(m+1)=m﹣2,
∴m=﹣4,
∴F'(﹣5,3),
即F對應點F′的坐標為(﹣5,3).



 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
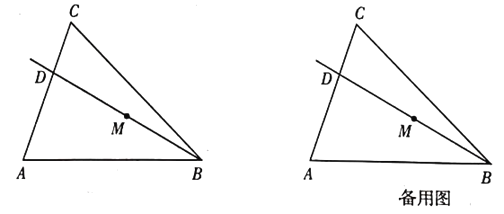
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,射線
,射線![]() 從與射線
從與射線![]() 重合的位置開始,繞點
重合的位置開始,繞點![]() 按順時針方向旋轉,與射線
按順時針方向旋轉,與射線![]() 重合時就停止旋轉,射線
重合時就停止旋轉,射線![]() 與線段
與線段![]() 相交于點
相交于點![]() ,點
,點![]() 是線段
是線段![]() 的中點.
的中點.
(1)求線段![]() 的長;
的長;
(2)①當點![]() 與點
與點![]() 、點
、點![]() 不重合時,過點
不重合時,過點![]() 作
作![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,連接
,連接![]() ,
,![]() ,在射線
,在射線![]() 旋轉的過程中,
旋轉的過程中,![]() 的大小是否發生變化?若不變,求
的大小是否發生變化?若不變,求![]() 的度數;若變化,請說明理由.
的度數;若變化,請說明理由.
②在①的條件下,連接![]() ,直接寫出
,直接寫出![]() 面積的最小值____________.
面積的最小值____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
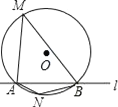
【題目】如圖,⊙O的半徑是2,直線l與⊙O相交于A、B兩點,M、N是⊙O上的兩個動點,且在直線l的異側,若∠AMB=45°,則四邊形MANB面積的最大值是( )
A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某物業公司計劃對所管理的小區3000m2區域進行綠化,經投標由甲、乙兩個工程隊來完成,甲、乙兩個工程隊每天共完成綠化面積150m2,甲隊完成600m2區域的綠化面積與乙隊完成300m2區域的綠化面積所用的天數相同.
(1)求甲、乙兩個工程隊每天各能完成多少面積的綠化?
(2)若甲隊每天綠化費用是0.6萬元,乙隊每天綠化費用是0.2萬元,該物業公司要使這次綠化總費用不超過17萬元,則至少安排乙工程隊綠化多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近期,某國遭遇了近年來最大的經濟危機,導致該國股市大幅震蕩,昨天某支股票累計賣出的數量和交易時間之間的關系如圖中虛線所示,累計買入的數量和交易時間之間的關系如圖中實線所示,其中點A是實線和虛線的交點,點C是BE的中點,CD與橫軸平行,則下列關于昨天該股票描述正確的是( )
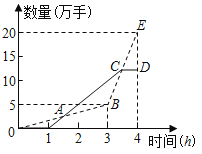
A.交易時間在3.5h時累計賣出的數量為12萬手
B.交易時間在1.4h時累計賣出和累計買入的數量相等
C.累計賣出的數量和累計買入的數量相差1萬手的時刻有5個
D.從點A對應的時刻到點C對應的時刻,平均每小時累計賣出的數量小于買入的數量
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線l1的解析式為![]() ,直線l2的解析式為
,直線l2的解析式為![]() ,與x軸、y軸分別交于點A、點B,直線l1與l2交于點C.
,與x軸、y軸分別交于點A、點B,直線l1與l2交于點C.
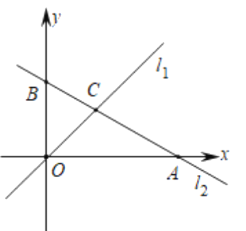

(1)求點A、點B、點C的坐標,并求出△COB的面積;
(2)若直線l2上存在點P(不與B重合),滿足S△COP=S△COB,請求出點P的坐標;
(3)在y軸右側有一動直線平行于y軸,分別與l1,l2交于點M、N,且點M在點N的下方,y軸上是否存在點Q,使△MNQ為等腰直角三角形?若存在,請直接寫出滿足條件的點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A,B,C都在拋物線y=ax2﹣2amx+am2﹣9(其中a>0)上,AB∥x軸,點P是拋物線的頂點,tan∠PBA=2,∠BAC=45°.
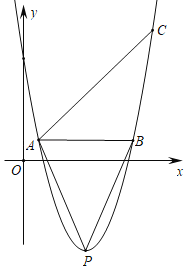
(1)填空:拋物線的頂點P的坐標為 (用含m的代數式表示);
(2)求△ABC的面積(用含a的代數式表示);
(3)若△ABC的面積為10,當2m﹣3≤x≤2m+5時,y的最小值為5,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“端午節”是我國的傳統佳節,民間歷來有吃“粽子”的習俗.我市某食品廠為了解市民對去年銷量較好的肉餡粽、豆沙餡粽、紅棗餡粽、蛋黃餡粽(以下分別用A,B,C,D表示)這四種不同口味粽子的喜愛情況,在節前對某居民區市民進行了抽樣調查,并將調查情況繪制成如下兩幅統計圖(尚不完整).
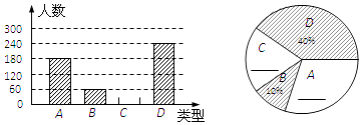
請根據以上信息回答:
(1)將兩幅不完整的圖補充完整;
(2)本次參加抽樣調查的居民有多少人?
(3)若居民區有8000人,請估計愛吃D粽的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,小橋用黑白棋子組成的一組圖案,第1個圖案由1個黑子組成,第2個圖案由1個黑子和6個白子組成,第3個圖案由13個黑子和6個白子組成,按照這樣的規律排列下去,則第9個圖案中共有( )和黑子.
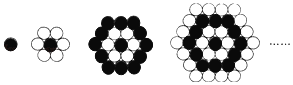
A.37B.42C.73D.121
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com