
【題目】如圖,一次函數y=-![]() x+2分別交y軸、x軸于A、B兩點,拋物線y=-
x+2分別交y軸、x軸于A、B兩點,拋物線y=-![]() +bx+c過A、B兩點.
+bx+c過A、B兩點.
(1)求這個拋物線的解析式;
(2)作垂直x軸的直線x=t,在第一象限交直線AB于M,交這個拋物線于N.求當t取何值時,MN有最大值?最大值是多少?
(3)在(2)的情況下,以A、M、N、D為頂點作平行四邊形,求第四個頂點D的坐標.
【答案】y=-![]() +3.5x+2;t=2時,最大值為4;(0,6),(0,-2)或(4,4)
+3.5x+2;t=2時,最大值為4;(0,6),(0,-2)或(4,4)
【解析】(1)首先求得A、B點的坐標,然后利用待定系數法求拋物線的解析式;
(2)本問要點是求得線段MN的表達式,這個表達式是關于t的二次函數,利用二次函數的極值求線段MN的最大值;
(3)本問要點是明確D點的可能位置有三種情形,如答圖2所示,不要遺漏.其中D1、D2在y軸上,利用線段數量關系容易求得坐標;D3點在第一象限,是直線D1N和D2M的交點,利用直線解析式求得交點坐標.
解:(1)∵![]() 分別交y軸、x軸于A、B兩點,
分別交y軸、x軸于A、B兩點,
∴A、B點的坐標為:A(0,2),B(4,0),
將x=0,y=2代入y=﹣x2+bx+c得c=2,
將x=4,y=0代入y=﹣x2+bx+c得0=﹣16+4b+2,解得b=![]() ,
,
∴拋物線解析式為:y=﹣x2+![]() x+2;
x+2;
(2)如答圖1,設MN交x軸于點E,
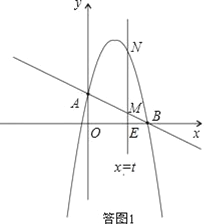
則E(t,0),BE=4﹣t.
∵tan∠ABO=![]() =
=![]() ,
,
∴ME=BEtan∠ABO=(4﹣t)×![]() =2﹣
=2﹣![]() t.
t.
又N點在拋物線上,且xN=t,∴yN=﹣t2+![]() t+2,
t+2,
∴MN=yN﹣ME=﹣t2+![]() t+2﹣(2﹣
t+2﹣(2﹣![]() t)=﹣t2+4t,
t)=﹣t2+4t,
∴當t=2時,MN有最大值4;
(3)由(2)可知,A(0,2),M(2,1),N(2,5).
以A、M、N、D為頂點作平行四邊形,D點的可能位置有三種情形,如答圖2所示.
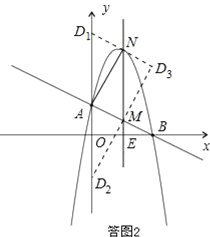
(i)當D在y軸上時,設D的坐標為(0,a)
由AD=MN,得|a﹣2|=4,解得a1=6,a2=﹣2,
從而D為(0,6)或D(0,﹣2),
(ii)當D不在y軸上時,由圖可知D3為D1N與D2M的交點,
易得D1N的方程為y=![]() x+6,D2M的方程為y=
x+6,D2M的方程為y=![]() x﹣2,
x﹣2,
由兩方程聯立解得D為(4,4)
故所求的D點坐標為(0,6),(0,﹣2)或(4,4).
“點睛”本題是二次函數綜合題,考查了拋物線上點的坐標特征、二次函數的極值、待定系數法求函數解析式、平行四邊形等重要知識點.難點在于第(3)問,點D的可能位置有三種情況,解答時年容易遺漏而導致失分,作為中考壓軸題此題有一定難度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】已知,直線在平面直角坐標系中與y軸交于點A,點B(﹣3,3)也在直線上,將點B先向右平移1個單位長度,再向下平移2個單位長度得到點C,點C也在直線上.求點A的坐標和直線的解析式;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用正方形硬紙板做三棱柱盒子,每個盒子由3個矩形側面和2個正三角形底面組成,硬紙板以如圖兩種方法裁剪(裁剪后邊角料不再利用).
A方法:剪6個側面; B方法:剪4個側面和5個底面.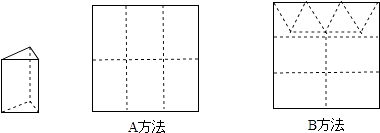
現有19張硬紙板,裁剪時x張用A方法,其余用B方法.
(1)用x的代數式分別表示裁剪出的側面和底面的個數;
(2)若裁剪出的側面和底面恰好全部用完,問能做多少個盒子?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為打造書香校園,計劃購進甲、乙兩種規格的書柜放置新購進的圖書,調查發現,若購買甲種書柜3個、乙種書柜2個,共需資金1020元;若購買甲種書柜4個,乙種書柜3個,共需資金1440元.
(1)甲、乙兩種書柜每個的價格分別是多少元?
(2)若該校計劃購進這兩種規格的書柜共20個,其中乙種書柜的數量不少于甲種書柜的數量,學校至多能夠提供資金4320元,請設計幾種購買方案供這個學校選擇.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在△ABC中,AB=AC=2![]() ,sinB=
,sinB=![]() ,D為邊BC的中點,E為邊BC的延長線上一點,且CE=BC,連結AE,F為線段AE的中點.
,D為邊BC的中點,E為邊BC的延長線上一點,且CE=BC,連結AE,F為線段AE的中點.
求:(1)線段DE的長;(2)tan∠CAE的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,直線CD切⊙O于點D,AM⊥CD于點M,連接AD,BD.
(1)求證:∠ADC=∠ABD;
(2)若AD=2![]() ,⊙O的半徑為3,求MD的長.
,⊙O的半徑為3,求MD的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com