
【題目】如圖,直線y=2x+3與x軸相交于點A,與y軸相交于點B.
(1)求A,B兩點的坐標;
(2)過B點作直線與x軸交于點P,若△ABP的面積為![]() ,試求點P的坐標.
,試求點P的坐標.

【答案】(1)A(﹣![]() ,0);(2)P點坐標為(1,0)或(﹣4,0)
,0);(2)P點坐標為(1,0)或(﹣4,0)
【解析】
試題(1)把x=0,y=0分別代入函數解析式,即可求得相應的y、x的值,則易得點A、B的坐標;
(2)由B、A的坐標易求:OB=3,OA=![]() .然后由三角形面積公式得到S△ABP=
.然后由三角形面積公式得到S△ABP=![]() APOB=
APOB=![]() ,則AP=
,則AP=![]() .設點P的坐標為(m,0),則m﹣(﹣
.設點P的坐標為(m,0),則m﹣(﹣![]() )=
)=![]() 或﹣
或﹣![]() ﹣m=
﹣m=![]() ,由此可以求得m的值.
,由此可以求得m的值.
試題解析:(1)由x=得:y=3,即:B(0,3).
由y=0得:2x+3=0,解得:x=﹣![]() ,即:A(﹣
,即:A(﹣![]() ,0);
,0);
(2)由B(0,3)、A(﹣![]() ,0)得:OB=3,OA=
,0)得:OB=3,OA=![]()
∵S△ABP=![]() APOB=
APOB=![]()
∴![]() AP=
AP=![]() ,
,
解得:AP=![]() .
.
設點P的坐標為(m,0),則m﹣(﹣![]() )=
)=![]() 或﹣
或﹣![]() ﹣m=
﹣m=![]() ,
,
解得:m=1或﹣4,
∴P點坐標為(1,0)或(﹣4,0).
 .
.


科目:初中數學 來源: 題型:
【題目】為了從甲、乙兩名同學中選拔一人參加射擊比賽,在同等的條件下,教練給甲、乙兩名同學安排了一次射擊測驗,每人打10發子彈,下面是甲、乙兩人各自的射擊情況記錄(其中乙的情況記錄表上射中9,10環的子彈數因被墨水污染而看不清楚,但是教練記得乙射中9,10環的子彈數均不為0發):
甲

乙

(1)求甲同學在這次測驗中平均每發射中的環數;
(2)根據這次測驗的情況,如果你是教練,你認為選誰參加比賽比較合適?并說明理由.(結果保留到小數點后1位)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為增強居民節約用水意識,某市在2018年開始對供水范圍內的居民用水實行“階梯收費”,具體收費標準如下表:

某戶居民四月份用水10 m3時,繳納水費23元.
(1) 求a的值;
(2) 若該戶居民五月份所繳水費為71元,求該戶居民五月份的用水量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是半圓O的直徑,點C在半圓O上,AB=4cm,∠CAB=60°,P是弧 ![]() 上的一個動點,連接AP,過C點作CD⊥AP于D,連接BD,在點P移動的過程中,BD的最小值是 .
上的一個動點,連接AP,過C點作CD⊥AP于D,連接BD,在點P移動的過程中,BD的最小值是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
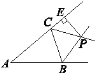
【題目】如圖,△ABC的兩條外角平分線BP,CP相交于點P,PE⊥AC交AC的延長線于點E.若△ABC的周長為11,PE=2,S△BPC=2,則S△ABC=________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線y=﹣x2+bx+c與x軸交于點A,B(A在B的左側),拋物線的對稱軸為直線x=1,AB=4. 
(1)求拋物線的表達式;
(2)拋物線上有兩點M(x1 , y1)和N(x2 , y2),若x1<1,x2>1,x1+x2>2,試判斷y1與y2的大小,并說明理由;
(3)直線l過A及C(0,﹣2),P為拋物線上一點(在x軸上方),過P作PD∥y軸交直線AC于點D,以PD為直徑作⊙E,求⊙E在直線AC上截得的線段的最大長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
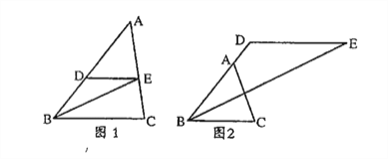
【題目】△ABC中,D是AB邊上的一點,過點D作DE∥BC,∠ABC的角平分線于點E.
(1)如圖1,當點E恰好在AC邊上時,求證:∠ADE=2∠DEB;
(2)如圖2,當點D在BA的延長線上時,其余條件不變,請直接寫出∠ADE與∠DEB之間的數量關系,并說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC和∠ACB的平分線相交于點F,過F作DE∥BC,交AB于點D,交AC于點E.若BD=4,DE=7,則線段EC的長為( )

A. 3 B. 4 C. 3.5 D. 2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com