
【題目】已知直角梯形ABCD中,AD∥BC,∠A=90°,△BCD為等邊三角形,且AD=![]() ,則梯形的周長(zhǎng)是_______.
,則梯形的周長(zhǎng)是_______.
【答案】![]() +5
+5![]() ;
;
【解析】
先根據(jù)△BCD是等邊三角形,可得∠2=60°,BC=CD=BD,而AD∥BC,∠A=90°,根據(jù)平行線的性質(zhì)可求∠ABC=90°,進(jìn)而可求∠1=30°,利用直角三角形中30°的角所對(duì)的直角邊等于斜邊的一半,易求BD,再根據(jù)勾股定理可求AB,從而可求梯形的周長(zhǎng).
如圖,
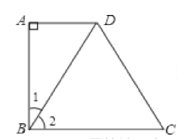
∵△BCD是等邊三角形,
∴∠2=60°,BC=CD=BD,
∵AD∥BC,∠A=90°,
∴∠ABC+∠A=180°,
∴∠ABC=90°,
∴∠1=90°60°=30°,
在Rt△ABD中,∵∠1=30°,AD=![]() ,
,
∴BD=2AD=2![]() ,AB=
,AB=![]() ,
,
∴梯形ABCD的周長(zhǎng)=AD+AB+BC+CD=![]() +
+![]() +2
+2![]() +2
+2![]() =
=![]() +5
+5![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】閱讀理解:若![]() 為數(shù)軸上三點(diǎn),若點(diǎn)
為數(shù)軸上三點(diǎn),若點(diǎn)![]() 到
到![]() 的距離是點(diǎn)
的距離是點(diǎn)![]() 到
到![]() 的距離的2倍,我們就稱(chēng)點(diǎn)
的距離的2倍,我們就稱(chēng)點(diǎn)![]() 是
是![]() 的優(yōu)點(diǎn). 例如圖1中:點(diǎn)
的優(yōu)點(diǎn). 例如圖1中:點(diǎn)![]() 表示的數(shù)為
表示的數(shù)為![]() ,點(diǎn)
,點(diǎn)![]() 表示的數(shù)為2. 表示1的點(diǎn)
表示的數(shù)為2. 表示1的點(diǎn)![]() 到點(diǎn)
到點(diǎn)![]() 的距離是2,到點(diǎn)
的距離是2,到點(diǎn)![]() 的距離是1,那么點(diǎn)
的距離是1,那么點(diǎn)![]() 是
是![]() 的優(yōu)點(diǎn);又如,表示0的點(diǎn)
的優(yōu)點(diǎn);又如,表示0的點(diǎn)![]() 到點(diǎn)
到點(diǎn)![]() 的距離是1,到點(diǎn)
的距離是1,到點(diǎn)![]() 的距離是2,那么點(diǎn)
的距離是2,那么點(diǎn)![]() 就不是
就不是![]() 的優(yōu)點(diǎn),但點(diǎn)
的優(yōu)點(diǎn),但點(diǎn)![]() 是
是![]() ,的優(yōu)點(diǎn).
,的優(yōu)點(diǎn).
知識(shí)運(yùn)用:(1)如圖2,![]() 為數(shù)軸上兩點(diǎn),點(diǎn)
為數(shù)軸上兩點(diǎn),點(diǎn)![]() 所表示的數(shù)為
所表示的數(shù)為![]() ,點(diǎn)
,點(diǎn)![]() 所表示的數(shù)為4. 那么數(shù)________所表示的點(diǎn)是
所表示的數(shù)為4. 那么數(shù)________所表示的點(diǎn)是![]() 的優(yōu)點(diǎn);(直接填在橫線上)
的優(yōu)點(diǎn);(直接填在橫線上)
(2)如圖3,![]() 為數(shù)軸上兩點(diǎn),點(diǎn)
為數(shù)軸上兩點(diǎn),點(diǎn)![]() 所表示的數(shù)為
所表示的數(shù)為![]() ,點(diǎn)
,點(diǎn)![]() 所表示的數(shù)為40. 現(xiàn)有一只電子螞蟻
所表示的數(shù)為40. 現(xiàn)有一只電子螞蟻![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),以4個(gè)單位每秒的速度向左運(yùn)動(dòng),到達(dá)點(diǎn)
出發(fā),以4個(gè)單位每秒的速度向左運(yùn)動(dòng),到達(dá)點(diǎn)![]() 停止. 當(dāng)
停止. 當(dāng)![]() 為何值時(shí),
為何值時(shí),![]() 、
、![]() 和
和![]() 中恰有一個(gè)點(diǎn)為其余兩點(diǎn)的優(yōu)點(diǎn)?
中恰有一個(gè)點(diǎn)為其余兩點(diǎn)的優(yōu)點(diǎn)?
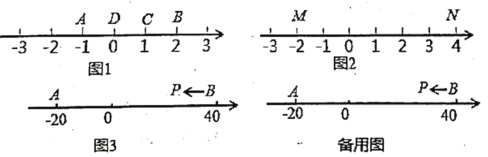
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】當(dāng)前,“精準(zhǔn)扶貧”工作已進(jìn)入攻堅(jiān)階段,凡貧困家庭均要“建檔立卡”![]() 某初級(jí)中學(xué)七年級(jí)共有四個(gè)班,已“建檔立卡”的貧困家庭的學(xué)生人數(shù)按一、二、三、四班分別記為
某初級(jí)中學(xué)七年級(jí)共有四個(gè)班,已“建檔立卡”的貧困家庭的學(xué)生人數(shù)按一、二、三、四班分別記為![]() ,
,![]() ,
,![]() ,
,![]() ,現(xiàn)對(duì)
,現(xiàn)對(duì)![]() ,
,![]() ,
,![]() ,
,![]() 統(tǒng)計(jì)后,制成如圖所示的統(tǒng)計(jì)圖.
統(tǒng)計(jì)后,制成如圖所示的統(tǒng)計(jì)圖.
![]() 求七年級(jí)已“建檔立卡”的貧困家庭的學(xué)生總?cè)藬?shù);
求七年級(jí)已“建檔立卡”的貧困家庭的學(xué)生總?cè)藬?shù);
![]() 將條形統(tǒng)計(jì)圖補(bǔ)充完整,并求出
將條形統(tǒng)計(jì)圖補(bǔ)充完整,并求出![]() 所在扇形的圓心角的度數(shù);
所在扇形的圓心角的度數(shù);
![]() 現(xiàn)從
現(xiàn)從![]() ,
,![]() 中各選出一人進(jìn)行座談,若
中各選出一人進(jìn)行座談,若![]() 中有一名女生,
中有一名女生,![]() 中有兩名女生,請(qǐng)用樹(shù)狀圖表示所有可能情況,并求出恰好選出一名男生和一名女生的概率.
中有兩名女生,請(qǐng)用樹(shù)狀圖表示所有可能情況,并求出恰好選出一名男生和一名女生的概率.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,點(diǎn)
中,點(diǎn)![]() 在
在![]() 軸的正半軸上,點(diǎn)
軸的正半軸上,點(diǎn)![]() 在直線
在直線![]() 上.
上.
(1)若點(diǎn)![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)連接![]() ,若點(diǎn)
,若點(diǎn)![]() ,
,![]() ,求
,求![]() 的長(zhǎng);
的長(zhǎng);
(3)過(guò)點(diǎn)![]() 作
作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,且交直線
,且交直線![]() 于點(diǎn)
于點(diǎn)![]() .若
.若![]() ,
,![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時(shí),求
時(shí),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
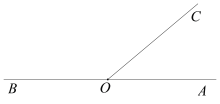
【題目】如圖,已知點(diǎn)O在直線AB上,作射線OC,點(diǎn)D在平面內(nèi),∠BOD與∠AOC互余.
(1)若∠AOC:∠BOD=4:5,則∠BOD= ;
(2)若∠AOC=α(0°<α≤45°),ON平分∠COD.
①當(dāng)點(diǎn)D在∠BOC內(nèi),補(bǔ)全圖形,直接寫(xiě)出∠AON的值(用含α的式子表示);
②若∠AON與∠COD互補(bǔ),求出α的值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在梯形ABCD中,AD∥BC,∠C=36°,∠B=54°,點(diǎn)M、N分別是AD、BC的中點(diǎn),如果BC=10,AD=4,那么MN的長(zhǎng)是___.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,正方形![]() 的邊
的邊![]() 在數(shù)軸上,數(shù)軸上點(diǎn)
在數(shù)軸上,數(shù)軸上點(diǎn)![]() 表示的數(shù)為
表示的數(shù)為![]() ,正方形
,正方形![]() 的面積為16.
的面積為16.
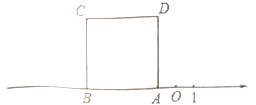
(1)數(shù)軸上點(diǎn)![]() 表示的數(shù)為__________;
表示的數(shù)為__________;
(2)將正方形![]() 沿?cái)?shù)軸水平移動(dòng),移動(dòng)后的正方形記為
沿?cái)?shù)軸水平移動(dòng),移動(dòng)后的正方形記為![]() ,移動(dòng)后的正方形
,移動(dòng)后的正方形![]() 與原正方形
與原正方形![]() 重疊部分的面積記為
重疊部分的面積記為![]() .當(dāng)
.當(dāng)![]() 時(shí),畫(huà)出圖形,并求出數(shù)軸上點(diǎn)
時(shí),畫(huà)出圖形,并求出數(shù)軸上點(diǎn)![]() 表示的數(shù);
表示的數(shù);
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
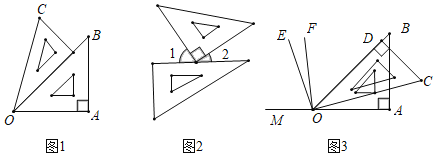
【題目】借助一副三角板,可以得到一些平面圖形
(1)如圖1,∠AOC= 度.由射線OA,OB,OC組成的所有小于平角的和是多少度?
(2)如圖2,∠1的度數(shù)比∠2度數(shù)的3倍還多30°,求∠2的度數(shù);
(3)利用圖3,反向延長(zhǎng)射線OA到M,OE平分∠BOM,OF平分∠COM,請(qǐng)按題意補(bǔ)全圖(3),并求出∠EOF的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】用如圖1所示的曲尺形框框(有三個(gè)方向),可以套住圖2日歷中的三個(gè)數(shù),設(shè)被框住的三個(gè)數(shù)中(第一個(gè)框框住的最大的數(shù)為![]() 、第二個(gè)框框住的最大的數(shù)為
、第二個(gè)框框住的最大的數(shù)為![]() 、第三個(gè)框框住的最大的數(shù)為
、第三個(gè)框框住的最大的數(shù)為![]() )
)

(1)第一個(gè)框框住的三個(gè)數(shù)的和是: ,第二個(gè)框框住的三個(gè)數(shù)的和是: ,第三個(gè)框框住的三個(gè)數(shù)中的和是: ;
(2)這三個(gè)框框住的數(shù)的和分別能是81嗎?若能,則分別求出最大的數(shù)![]() 、
、![]() 、
、![]() .
.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com