
【題目】借助一副三角板,可以得到一些平面圖形
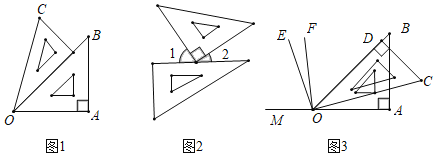
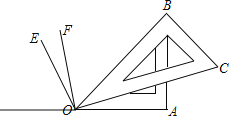
(1)如圖1,∠AOC= 度.由射線OA,OB,OC組成的所有小于平角的和是多少度?
(2)如圖2,∠1的度數比∠2度數的3倍還多30°,求∠2的度數;
(3)利用圖3,反向延長射線OA到M,OE平分∠BOM,OF平分∠COM,請按題意補全圖(3),并求出∠EOF的度數.
【答案】(1)75°,150°;(2)15°;(3)15°.
【解析】
(1)根據三角板的特殊性角的度數,求出∠AOC即可,把∠AOC、∠BOC、∠AOB相加即可求出射線OA,OB,OC組成的所有小于平角的和;
(2)依題意設∠2=x,列等式,解方程求出即可;
(3)依據題意求出∠BOM,∠COM,再根據角平分線的性質得出∠MOE,∠MOF,即可求出∠EOF.
解:(1)∵∠BOC=30°,∠AOB=45°,
∴∠AOC=75°,
∴∠AOC+∠BOC+∠AOB=150°;
答:由射線OA,OB,OC組成的所有小于平角的和是150°;
故答案為:75;
(2)設∠2=x,則∠1=3x+30°,
∵∠1+∠2=90°,
∴x+3x+30°=90°,
∴x=15°,
∴∠2=15°,
答:∠2的度數是15°;
(3)如圖所示,∵∠BOM=180°﹣45°=135°,∠COM=180°﹣15°=165°,
∵OE為∠BOM的平分線,OF為∠COM的平分線,
∴∠MOF=![]() ∠COM=82.5°,∠MOE=
∠COM=82.5°,∠MOE=![]() ∠MOB=67.5°,
∠MOB=67.5°,
∴∠EOF=∠MOF﹣∠MOE=15°.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
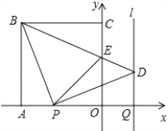
【題目】如圖,正方形OABC的邊OA,OC在坐標軸上,點B的坐標為(﹣4,4).點P從點A出發(fā),以每秒1個單位長度的速度沿x軸向點O運動;點Q從點O同時出發(fā),以相同的速度沿x軸的正方向運動,規(guī)定點P到達點O時,點Q也停止運動.連接BP,過P點作BP的垂線,與過點Q平行于y軸的直線l相交于點D.BD與y軸交于點E,連接PE.設點P運動的時間為t(s).
(1)∠PBD的度數為 ,點D的坐標為 (用t表示);
(2)當t為何值時,△PBE為等腰三角形?
(3)探索△POE周長是否隨時間t的變化而變化?若變化,說明理由;若不變,試求這個定值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=BC,點O在AB上,經過點A的⊙O與BC相切于點D,交AB于點E.
(1)求證:AD平分∠BAC;
(2)若CD=1,求圖中陰影部分的面積(結果保留π).

查看答案和解析>>
科目:初中數學 來源: 題型:
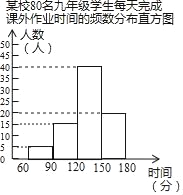
【題目】為了解九年級課業(yè)負擔情況,某校隨機抽取80名九年級學生進行問卷調查,在整理并匯總這80張有效問卷的數據時發(fā)現,每天完成課外作業(yè)時間,最長不超過180分鐘,最短不少于60分鐘,并將調查結果繪制成如圖所示的頻數分布直方圖.
(1)被調查的80名學生每天完成課外作業(yè)時間的中位數在_____組(填時間范圍).
(2)該校九年級共有800名學生,估計大約有_____名學生每天完成課外作業(yè)時間在120分鐘以上(包括120分鐘)
查看答案和解析>>
科目:初中數學 來源: 題型:
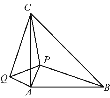
【題目】如圖,在等腰△ABC中,∠CAB=90°,P是△ABC內一點,PA=1,PB=3,PC=![]() ,將△APB繞點A逆時針旋轉后與△AQC重合.求:
,將△APB繞點A逆時針旋轉后與△AQC重合.求:
(1)線段PQ的長;
(2)∠APC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長是3,BP=CQ,連接AQ,DP交于點O,并分別與邊CD,BC交于點F,E,連接AE,下列結論:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四邊形OECF;④當BP=1時,tan∠OAE=![]() ,其中正確結論的個數是( )
,其中正確結論的個數是( )
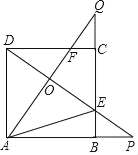
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于方程![]() =1,某同學解法如下:
=1,某同學解法如下:
解:方程兩邊同乘6,得3x﹣2(x﹣1)=1 ①
去括號,得3x﹣2x﹣2=1 ②
合并同類項,得x﹣2=1 ③
解得x=3 ④
∴原方程的解為x=3 ⑤
(1)上述解答過程中的錯誤步驟有 (填序號);
(2)請寫出正確的解答過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
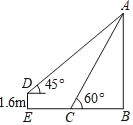
【題目】小明想利用所學數學知識測量學校旗桿高度,如圖,旗桿的頂端垂下一繩子,將繩子拉直釘在地上,末端恰好在C處且與地面成60°角,小明拿起繩子末端,后退至E處,拉直繩子,此時繩子末端D距離地面1.6m且繩子與水平方向成45°角.
(1)填空:AD_____AC(填“>”,“<”,“=”).
(2)求旗桿AB的高度.
(參考數據: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,結果精確到0.1m).
≈1.73,結果精確到0.1m).
查看答案和解析>>
科目:初中數學 來源: 題型:
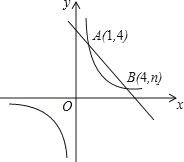
【題目】如圖,一次函數y=kx+b與反比例函數y=![]() 的圖象交于A(1,4),B(4,n)兩點.
的圖象交于A(1,4),B(4,n)兩點.
(1)求反比例函數和一次函數的解析式;
(2)點P是x軸上的一動點,試確定點P并求出它的坐標,使PA+PB最小.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com