
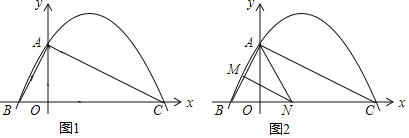
【題目】如圖1,已知二次函數y=ax2+![]() x+c(a≠0)的圖象與y軸交于點A(0,4),與x軸交于點B、C,點C坐標為(8,0),連接AB、AC.
x+c(a≠0)的圖象與y軸交于點A(0,4),與x軸交于點B、C,點C坐標為(8,0),連接AB、AC.
(1)請直接寫出二次函數y=ax2+![]() x+c的表達式;
x+c的表達式;
(2)判斷△ABC的形狀,并說明理由;
(3)若點N在x軸上運動,當以點A、N、C為頂點的三角形是等腰三角形時,請寫出此時點N的坐標;
(4)如圖2,若點N在線段BC上運動(不與點B、C重合),過點N作NM∥AC,交AB于點M,當△AMN面積最大時,求此時點N的坐標.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)△ABC是直角三角形.理由見解析;(3)點N的坐標分別為(﹣8,0)、(8﹣4
x+4;(2)△ABC是直角三角形.理由見解析;(3)點N的坐標分別為(﹣8,0)、(8﹣4![]() ,0)、(3,0)、(8+4
,0)、(3,0)、(8+4![]() ,0).(4)當△AMN面積最大時,N點坐標為(3,0).
,0).(4)當△AMN面積最大時,N點坐標為(3,0).
【解析】
(1)由點A、C的坐標利用待定系數法即可求出二次函數的解析式;(2)令二次函數解析式中y=0,求出點B的坐標,再由兩點間的距離公式求出線段AB、AC、BC的長度,由三者滿足AB2+AC2=BC2即可得出△ABC為直角三角形;(3)分別以A、C兩點為圓心,AC長為半徑畫弧,與x軸交于三個點,由AC的垂直平分線與x軸交于一點,即可求得點N的坐標;(4)設點N的坐標為(n,0)(-2<n<8),通過分割圖形法求面積,再根據相似三角形面積間的關系以及三角形的面積公式即可得出S△AMN關于n的二次函數關系式,根據二次函數的性質即可解決最值問題.
(1)∵二次函數y=ax2+![]() x+c的圖象與y軸交于點A(0,4),與x軸交于點B、C,點C坐標為(8,0),
x+c的圖象與y軸交于點A(0,4),與x軸交于點B、C,點C坐標為(8,0),
∴![]() ,
,
解得![]() .
.
∴拋物線表達式:y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)△ABC是直角三角形.
令y=0,則﹣![]() x2+
x2+![]() x+4=0,
x+4=0,
解得x1=8,x2=﹣2,
∴點B的坐標為(﹣2,0),
由已知可得,
在Rt△ABO中AB2=BO2+AO2=22+42=20,
在Rt△AOC中AC2=AO2+CO2=42+82=80,
又∵BC=OB+OC=2+8=10,
∴在△ABC中AB2+AC2=20+80=102=BC2
∴△ABC是直角三角形.
(3)∵A(0,4),C(8,0),
∴AC=![]() =4
=4![]() ,
,
①以A為圓心,以AC長為半徑作圓,交x軸于N,此時N的坐標為(﹣8,0),
②以C為圓心,以AC長為半徑作圓,交x軸于N,此時N的坐標為(8﹣4![]() ,0)或(8+4
,0)或(8+4![]() ,0)
,0)
③作AC的垂直平分線,交x軸于N,此時N的坐標為(3,0),
綜上,若點N在x軸上運動,當以點A、N、C為頂點的三角形是等腰三角形時,點N的坐標分別為(﹣8,0)、(8﹣4![]() ,0)、(3,0)、(8+4
,0)、(3,0)、(8+4![]() ,0).
,0).
(4)如圖
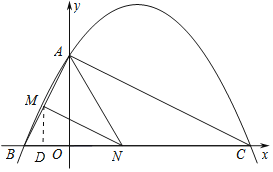 ,
,
設點N的坐標為(n,0),則BN=n+2,過M點作MD⊥x軸于點D,
∴MD∥OA,
∴△BMD∽△BAO,
∴![]() =
=![]() ,
,
∵MN∥AC
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵OA=4,BC=10,BN=n+2
∴MD=![]() (n+2),
(n+2),
∵S△AMN=S△ABN﹣S△BMN
=![]() BNOA﹣
BNOA﹣![]() BNMD
BNMD
=![]() (n+2)×4﹣
(n+2)×4﹣![]() ×
×![]() (n+2)2
(n+2)2
=﹣![]() (n﹣3)2+5,
(n﹣3)2+5,
當n=3時,△AMN面積最大是5,
∴N點坐標為(3,0).
∴當△AMN面積最大時,N點坐標為(3,0).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】“六一”兒童節前夕,某部隊戰士到福利院慰問兒童.戰士們從營地出發,勻速步行前往文具店選購禮物,停留一段時間后,繼續按原速步行到達福利院(營地、文具店、福利院三地依次在同一直線上).到達后因接到緊急任務,立即按原路勻速跑步返回營地(贈送禮物的時間忽略不計),下列圖象能大致反映戰
士們離營地的距離![]() 與時間
與時間![]() 之間函數關系的是( )
之間函數關系的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
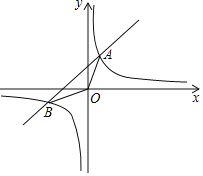
【題目】如圖,已知一次函數y=kx+b(k≠0)與反比例函數y=![]() (m≠0)的圖象相交于A、B兩點,且點A的坐標是(1,2),點B的坐標是(﹣2,w).
(m≠0)的圖象相交于A、B兩點,且點A的坐標是(1,2),點B的坐標是(﹣2,w).
(1)求一次函數與反比例函數的解析式;
(2)在x軸的正半軸上找一點C,使△AOC的面積等于△ABO的面積,并求出點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一根長為![]() 的鐵絲剪成兩段,并把每一段鐵絲圍成一個正方形.若設圍成的一個正方形的邊長為
的鐵絲剪成兩段,并把每一段鐵絲圍成一個正方形.若設圍成的一個正方形的邊長為![]() .
.
(1)要使這兩個正方形的面積的和等于![]() ,則剪出的兩段鐵絲長分別是多少?
,則剪出的兩段鐵絲長分別是多少?
(2)剪出的兩段鐵絲長分別是多少![]() 時,這兩個正方形的面積和最小?最小值是多少?
時,這兩個正方形的面積和最小?最小值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,可以自由轉動的轉盤被它的兩條直徑分成了四個分別標有數字的扇形區域,其中標有數字“1”的扇形圓心角為120°.轉動轉盤,待轉盤自動停止后,指針指向一個扇形的內部,則該扇形內的數字即為轉出的數字,此時,稱為轉動轉盤一次(若指針指向兩個扇形的交線,則不計轉動的次數,重新轉動轉盤,直到指針指向一個扇形的內部為止)
(1)轉動轉盤一次,求轉出的數字是-2的概率;
(2)轉動轉盤兩次,用樹狀圖或列表法求這兩次分別轉出的數字之積為正數的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線![]() 分別交
分別交![]() 軸、
軸、![]() 軸于點
軸于點![]() 、
、![]() ,拋物線過
,拋物線過![]() ,
,![]() 兩點,點
兩點,點![]() 是線段
是線段![]() 上一動點,過點
上一動點,過點![]() 作
作![]() 軸于點
軸于點![]() ,交拋物線于點
,交拋物線于點![]() .
.

(1)若拋物線的頂點![]() 的坐標為
的坐標為![]() ,其對稱軸交
,其對稱軸交![]() 于點
于點![]() ,
,
①求拋物線的解析式;
②是否存在點![]() ,使四邊形
,使四邊形![]() 為菱形?并說明理由;
為菱形?并說明理由;
(2)當點![]() 的橫坐標為1時,是否存在這樣的拋物線,使得以
的橫坐標為1時,是否存在這樣的拋物線,使得以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,求出滿足條件的拋物線的解析式:若不存在,請說明理由.
相似?若存在,求出滿足條件的拋物線的解析式:若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,用直尺和圓規作∠BAD的平分線AG交BC于點E,若BF=6,AB=4,則AE的長為( )
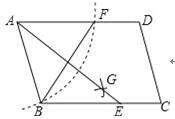
A. ![]() B. 2
B. 2![]() C. 3
C. 3![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的盒子里,裝有5個分別標有數字1,2,3,4,5的小球,它們的形狀、大小、質地等完全相同.雄威同學先從盒子里隨機取出第一個小球,記下數字為x;不放回盒子,再由麗賢同學隨機取出第二個小球,記下數字為y.
(1)請用樹狀圖或列表法表示出坐標(x,y)的所有可能出現的結果;
(2)求雄威同學、麗賢同學各取一個小球所確定的點(x,y)落在反比例函數y=![]() 的圖象上的概率.
的圖象上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 某蛋糕店出售網紅“奶昔包”,成本為30元/件,每天銷售y(件)與銷售單價x(元)之間存在一次函數關系,當以40元每件出售時,每天可以賣300件,當以55元每件出售時,每天可以賣150件.
(1)求y與x之間的函數關系式;
(2)如果規定每天“奶昔包”的銷售量不低于240件,當銷售單價為多少元時,每天獲取的利潤最大,最大利潤是多少?
(3)該蛋糕店店主熱心公益事業,決定從每天的銷售利潤中捐出150元給希望工程,為了保證捐款后每天剩余利潤不低于3600元,試直接寫出該“奶昔包”銷售單價的范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com