
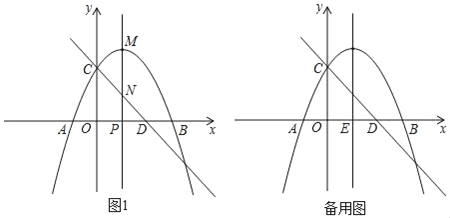
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側(cè)),點
的左側(cè)),點![]() 的坐標為
的坐標為![]() ,與
,與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() .動點
.動點![]() 在拋物線上運動,過點
在拋物線上運動,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,交直線
,交直線![]() 于點
于點![]() .
.
(1)求拋物線的解析式;
(2)當點![]() 在線段
在線段![]() 上時,
上時,![]() 的面積是否存在最大值,若存在,請求出最大值;若不存在,請說明理由;
的面積是否存在最大值,若存在,請求出最大值;若不存在,請說明理由;
(3)點![]() 是拋物線對稱軸與
是拋物線對稱軸與![]() 軸的交點,點
軸的交點,點![]() 是
是![]() 軸上一動點,點
軸上一動點,點![]() 在運動過程中,若以
在運動過程中,若以![]() 為頂點的四邊形是平行四邊形時,請直接寫出點
為頂點的四邊形是平行四邊形時,請直接寫出點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)存在.當
;(2)存在.當![]() 時,
時,![]() 有最大值為
有最大值為![]() ;(3)
;(3)![]() 點坐標為
點坐標為![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用待定系數(shù)法求拋物線的解析式;
(2)設(shè)![]() ,則
,則![]() ,則
,則![]() ,根據(jù)三角形面積公式得到
,根據(jù)三角形面積公式得到![]() ,然后根據(jù)二次函數(shù)的性質(zhì)解決問題;
,然后根據(jù)二次函數(shù)的性質(zhì)解決問題;
(3)先求出拋物線的對稱軸為直線![]() 得到
得到![]() ,討論:當
,討論:當![]() 時,則
時,則![]() ,利用平行四邊形的性質(zhì)得
,利用平行四邊形的性質(zhì)得![]() ,從而得到此時
,從而得到此時![]() 點坐標;當
點坐標;當![]() 時,由于點
時,由于點![]() 向右平移
向右平移![]() 個單位,向下平移
個單位,向下平移![]() 個單位得到
個單位得到![]() 點,所以點
點,所以點![]() 向右平移
向右平移![]() 個單位,向下平移
個單位,向下平移![]() 個單位得到
個單位得到![]() 點,設(shè)
點,設(shè)![]() ,則
,則![]() ,然后把
,然后把![]() 代入
代入![]() 得
得![]() ,則解方程求出得到此時
,則解方程求出得到此時![]() 點坐標.
點坐標.
解:(1)![]() 拋物線經(jīng)過點
拋物線經(jīng)過點![]() ,點
,點![]() ,
,
 ,解得
,解得![]() ,
,
![]() 拋物線的解析式為
拋物線的解析式為![]() ;
;
(2)存在.
當![]() ,解得
,解得![]() ,則
,則![]() ,
,
設(shè)![]() ,則
,則![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() 當
當![]() 時,
時,![]() 有最大值為
有最大值為![]() ;
;
(3)![]() 拋物線的對稱軸為直線
拋物線的對稱軸為直線 ,
,
![]() ,
,
當![]() 時,則
時,則![]() ,
,
![]() 以
以![]() 為頂點的四邊形是平行四邊形,
為頂點的四邊形是平行四邊形,
![]() ,
,
![]() 點坐標為
點坐標為![]() 或
或![]()
當![]() 時,
時,
![]() 以
以![]() 為頂點的四邊形是平行四邊形,
為頂點的四邊形是平行四邊形,
![]() ,
,
![]() 點
點![]() 向右平移
向右平移![]() 個單位,向下平移
個單位,向下平移![]() 個單位得到
個單位得到![]() 點,
點,
![]() 點
點![]() 向右平移
向右平移![]() 個單位,向下平移
個單位,向下平移![]() 個單位得到
個單位得到![]() 點,
點,
設(shè)![]() ,則
,則![]() ,
,
把![]() 代入
代入![]() 得
得![]() ,解得
,解得![]() ,
,
此時![]() 點坐標為
點坐標為![]() ,
,
綜上所述,![]() 點坐標為
點坐標為![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校初三(1)班部分同學(xué)接受一次內(nèi)容為“最適合自己的考前減壓方式”的調(diào)查活動,收集整理數(shù)據(jù)后,老師將減壓方式分為五類,并繪制了圖1、圖2兩個不完整的統(tǒng)計圖,請根據(jù)圖中的信息解答下列問題.
(1)初三(1)班接受調(diào)查的同學(xué)共有多少名;
(2)補全條形統(tǒng)計圖,并計算扇形統(tǒng)計圖中的“體育活動C”所對應(yīng)的圓心角度數(shù);
(3)若喜歡“交流談心”的5名同學(xué)中有三名男生和兩名女生;老師想從5名同學(xué)中任選兩名同學(xué)進行交流,直接寫出選取的兩名同學(xué)都是女生的概率.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標系中,A,B兩點的縱坐標分別為7和1,直線AB與y軸所夾銳角為60°.
(1)求線段AB的長;
(2)求經(jīng)過A,B兩點的反比例函數(shù)的解析式.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
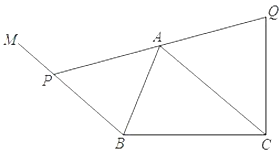
【題目】已知:如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() .過點
.過點![]() 作
作![]() ,動點
,動點![]() 在射線
在射線![]() 上(點
上(點![]() 不與
不與![]() 重合),聯(lián)結(jié)
重合),聯(lián)結(jié)![]() 并延長到點
并延長到點![]() ,使
,使![]() .
.
(1)求![]() 的面積;
的面積;
(2)設(shè)![]() ,
,![]() ,求
,求![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式,并寫出
的函數(shù)解析式,并寫出![]() 的取值范圍;
的取值范圍;
(3)連接![]() ,如果
,如果![]() 是直角三角形,求
是直角三角形,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
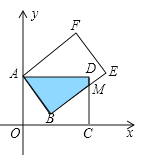
【題目】(12分)矩形AOCD繞頂點A(0,5)逆時針方向旋轉(zhuǎn),當旋轉(zhuǎn)到如圖所示的位置時,邊BE交邊CD于M,且ME=2,CM=4.
(1)求AD的長;
(2)求陰影部分的面積和直線AM的解析式;
(3)求經(jīng)過A、B、D三點的拋物線的解析式;
(4)在拋物線上是否存在點P,使![]() ?若存在,求出P點坐標;若不存在,請說明理由.
?若存在,求出P點坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,兩個全等的△ABC和△DEF中,∠ACB=∠DFE=90°,AB=DE,其中點B和點D重合,點F在BC上,將△DEF沿射線BC平移,設(shè)平移的距離為x,平移后的圖形與△ABC重合部分的面積為y,y關(guān)于x的函數(shù)圖象如圖2所示(其中0≤x≤m,m<x≤3,3<x≤4時,函數(shù)的解析式不同)
(1)填空:BC的長為_____;
(2)求y關(guān)于x的函數(shù)關(guān)系式,并寫出x的取值范圍.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
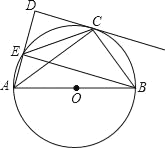
【題目】如圖,AB是⊙O的直徑,CD切⊙O于點C,AD交⊙O于點E,AC平分∠BAD,連接BE.
(1)求證:CD⊥ED;
(2)若CD=4,AE=2,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為落實“美麗撫順”的工作部署,市政府計劃對城區(qū)道路進行了改造,現(xiàn)安排甲、乙兩個工程隊完成.已知甲隊的工作效率是乙隊工作效率的![]() 倍,甲隊改造360米的道路比乙隊改造同樣長的道路少用3天.
倍,甲隊改造360米的道路比乙隊改造同樣長的道路少用3天.
(1)甲、乙兩工程隊每天能改造道路的長度分別是多少米?
(2)若甲隊工作一天需付費用7萬元,乙隊工作一天需付費用5萬元,如需改造的道路全長1200米,改造總費用不超過145萬元,至少安排甲隊工作多少天?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖分別是某款籃球架的實物圖與示意圖,已知![]() 于點
于點![]() ,底座
,底座![]() 的長為
的長為![]() 米,底座
米,底座![]() 與支架
與支架![]() 所成的角
所成的角![]() ,點
,點![]() 在支架
在支架![]() 上,籃板底部支架
上,籃板底部支架![]() 于點
于點![]() ,已知
,已知![]() 長
長![]() 米,
米,![]() 長
長![]() 米,
米,![]() 長
長![]() 米.
米.
(1)求籃板底部支架![]() 與
與![]() 支架所成的角
支架所成的角![]() 的度數(shù).
的度數(shù).
(2)求籃板底部點![]() 到地面的距離.(結(jié)果保留根號)
到地面的距離.(結(jié)果保留根號)

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com