
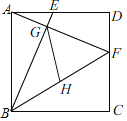
【題目】已知正方形ABCD的邊長為4,點E,F分別在AD,DC上,AE=DF=1,BE與AF相交于點G,點H為BF的中點,連接GH,則GH的長為_____.
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知正比例函數y=![]() x的圖象與反比例函數y=
x的圖象與反比例函數y=![]() 的圖象交于A(a,-2),B兩點.
的圖象交于A(a,-2),B兩點.
(1)求反比例函數的表達式和點B的坐標;
(2)P是第一象限內反比例函數圖象上一點,過點P作y軸的平行線,交直線AB于點C,連接PO,若△POC的面積為3,求點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是平行四邊形,點A(1,0),B(3,1),C(3,3).反比例函數y=![]() (x>0)的圖像經過點D,P是一次函數y=kx+3-3k(k≠0)的圖像與該反比例函數圖像的一個公共點.
(x>0)的圖像經過點D,P是一次函數y=kx+3-3k(k≠0)的圖像與該反比例函數圖像的一個公共點.
(1)求反比例函數的表達式;
(2)通過計算說明一次函數y=kx+3-3k(k≠0)的圖像一定經過點C;
(3)對于一次函數y=kx+3-3k(k≠0),當y隨x的增大而增大時,確定點P的橫坐標的取值范圍(不必寫出過程).

查看答案和解析>>
科目:初中數學 來源: 題型:
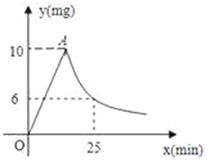
【題目】由于天氣炎熱,某校根據《學校衛生工作條例》,為預防“蚊蟲叮咬”,對教室進行“薰藥消毒”.已知藥物在燃燒機釋放過程中,室內空氣中每立方米含藥量y(毫克)與燃燒時間x(分鐘)之間的關系如圖所示(即圖中線段OA和雙曲線在A點及其右側的部分),當空氣中每立方米的含藥量低于2毫克時,對人體無毒害作用,那么從消毒開始,至少在_______分鐘內,師生不能呆在教室.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=4cm,∠ADC=120°,點E、F同時由A、C兩點出發,分別沿AB、CB方向向點B勻速移動(到點B為止),點E的速度為1cm/s,點F的速度為2cm/s,經過t秒△DEF為等邊三角形,則t的值為( )
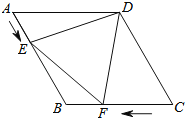
A. 1sB. ![]() sC.
sC. ![]() sD. 2s
sD. 2s
查看答案和解析>>
科目:初中數學 來源: 題型:
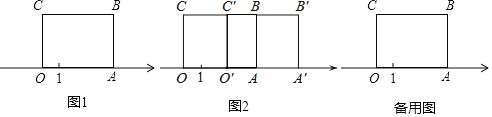
【題目】如圖1,長方形![]() 的邊
的邊![]() 在數軸上,
在數軸上,![]() 為原點,長方形
為原點,長方形![]() 的面積為12,
的面積為12,![]() 邊長為3.
邊長為3.
(1)數軸上點![]() 表示的數為____________.
表示的數為____________.
(2)將長方形![]() 沿數軸水平移動,移動后的長方形記為
沿數軸水平移動,移動后的長方形記為![]() ,移動后的長方形
,移動后的長方形![]() 與原長方形
與原長方形![]() 重疊部分(如圖2中陰影部分)的面積記為
重疊部分(如圖2中陰影部分)的面積記為![]() .
.
① 當![]() 恰好等于原長方形
恰好等于原長方形![]() 面積的一半時,數軸上點
面積的一半時,數軸上點![]() 表示的數為____________
表示的數為____________
② 設點![]() 的移動距離
的移動距離![]()
ⅰ. 當![]() 時,
時,![]() __________;
__________;
ⅱ. D為線段![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上,且
上,且![]() ,當點
,當點![]() 所表示的數互為相反數時,求
所表示的數互為相反數時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,對角線AC、BD相交于點O,AD=![]() DB,點E、F、G分別是AO、BO、DC的中點,連接EF、DE、EG、GF.
DB,點E、F、G分別是AO、BO、DC的中點,連接EF、DE、EG、GF.
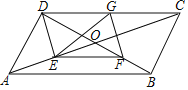
(1)求證:四邊形DEFG是平行四邊形;
(2)求證:EG=EF.
查看答案和解析>>
科目:初中數學 來源: 題型:
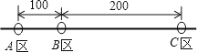
【題目】某公司員工分別在A、B、C三個住宅區,A區有30人,B區有15人,C,區有10人,三個區在一直線上,位置如圖所示,公司的接送車打算在此間只設一個停靠點,為要使所有員工步行到停靠點的路程總和最少,那么停靠點的位置應在_____區.
查看答案和解析>>
科目:初中數學 來源: 題型:
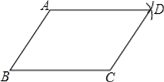
【題目】嘉琪同學要證明命題“兩組對邊分別相等的四邊形是平行四邊形”是正確的,她先用尺規作出了如圖所示的□ABCD,并寫出了如下尚不完整的已知和求證.
已知:如圖,在四邊形ABCD中,BC=AD,AB= .
求證:四邊形ABCD是 四邊形.
(1)補全已知和求證(在方框中填空);
(2)嘉琪同學想利用三角形全等,依據“兩組對邊分別平行的四邊形是平行四邊形”來證明.請你按她的想法完成證明過程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com