Question

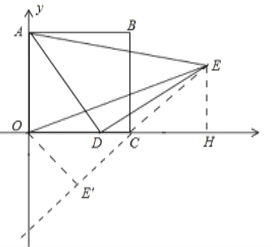
【題目】如圖，在平面直角坐標系中，已知正方形 ABCO，邊長是 4，點 D(a，0)，以 AD 為邊在AD 的右側作等腰 Rt△ADE，∠ADE＝90°，連接 OE，則 OE 的最小值為__________________．

Answer 1

【答案】

【解析】

如圖，作EH⊥x軸于H，連接CE．利用全等三角形的性質證明∠ECH＝45°，推出點E在直線y＝x4上運動，作OE′⊥CE，求出OE′的長即可解決問題；

如圖，作EH⊥x軸于H，連接CE．

∵∠AOD＝∠ADE＝∠EHD＝90°，

∴∠ADO＋∠EDH＝90°，∠EDH＋∠DEH＝90°，

∴∠ADO＝∠DEH，

∵AD＝DE，

∴△ADO≌△DEH（AAS），

∴OA＝DH＝OC=4，OD＝EH，

∴OD＝CH＝EH，

∴∠ECH＝45°，

故可設CE直線的解析式為y=x+b

把C（4,0）代入得0=4+b

解得b=-4

∴CE直線的解析式為y=x-4

∴點E在直線y＝x4上運動，作OE′⊥CE，則△OCE′是等腰直角三角形，

∴CE’=OE’

∵OC＝4，

∴CE’2+OE’2=OC2，

即2OE’2=42，

解得OE′＝，

∴OE的最小值為．

故答案為：．