
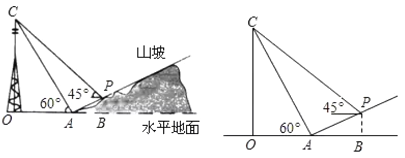
【題目】如圖,某人在山坡坡腳![]() 處測(cè)得電視塔尖點(diǎn)
處測(cè)得電視塔尖點(diǎn)![]() 的仰角為
的仰角為![]() ,沿山坡向上走到
,沿山坡向上走到![]() 處再測(cè)得點(diǎn)
處再測(cè)得點(diǎn)![]() 的仰角為
的仰角為![]() ,已知
,已知![]() 米,山坡坡度
米,山坡坡度![]() ,且
,且![]() 在同一條直線上,其中測(cè)傾器高度忽略不計(jì).
在同一條直線上,其中測(cè)傾器高度忽略不計(jì).
(1)求電視塔![]() 的高度;(計(jì)算結(jié)果保留根號(hào)形式)
的高度;(計(jì)算結(jié)果保留根號(hào)形式)
(2)求此人所在位置點(diǎn)![]() 的鉛直高度.(結(jié)果精確到0.1米,參考數(shù)據(jù):
的鉛直高度.(結(jié)果精確到0.1米,參考數(shù)據(jù):![]() ,
,![]() )
)
【答案】(1)電視塔![]() 的高度為
的高度為![]() 米;(2)此人所在位置點(diǎn)
米;(2)此人所在位置點(diǎn)![]() 的鉛直高度約為24.3米.
的鉛直高度約為24.3米.
【解析】
(1)根據(jù)![]() 、
、![]() ,由三角函數(shù)可以求解出電視塔
,由三角函數(shù)可以求解出電視塔![]() 的高度;
的高度;
(2)構(gòu)造矩形![]() ,把求人所在位置點(diǎn)
,把求人所在位置點(diǎn)![]() 的鉛直高度轉(zhuǎn)化成求矩形OF的邊長(zhǎng),通過假設(shè)PB的長(zhǎng)度,得到含未知數(shù)的方程式進(jìn)而求解
的鉛直高度轉(zhuǎn)化成求矩形OF的邊長(zhǎng),通過假設(shè)PB的長(zhǎng)度,得到含未知數(shù)的方程式進(jìn)而求解
解:(1)在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
答:電視塔![]() 的高度為
的高度為![]() 米;
米;
(2)如圖,過點(diǎn)![]() 作
作![]() ,垂足為
,垂足為![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() ,垂足為
,垂足為![]() ,
,
則四邊形![]() 是矩形,
是矩形,
![]() (矩形對(duì)邊相等).
(矩形對(duì)邊相等).
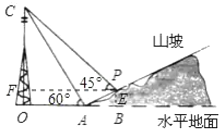
由![]() ,設(shè)
,設(shè)![]() 米,則
米,則![]() ,
,
![]() ,
,
在![]() 中,由
中,由![]() ,
,
∴![]() 是的等腰直角三角形,
是的等腰直角三角形,
![]() ,即
,即![]() ,
,
![]() .
.
即![]() 米,
米,
答:此人所在位置點(diǎn)![]() 的鉛直高度約為24.3米.
的鉛直高度約為24.3米.


 陽光試卷單元測(cè)試卷系列答案
陽光試卷單元測(cè)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC.
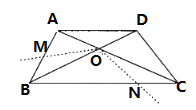
(1)求出sin∠DBC的值;
(2)若AD=2,把∠BOC繞點(diǎn)O順時(shí)針旋轉(zhuǎn)![]() (
(![]() ),交AB于點(diǎn)M,交BC于點(diǎn)N(如圖),求證:四邊形OMBN的面積為一個(gè)定值,并求出這個(gè)定值.
),交AB于點(diǎn)M,交BC于點(diǎn)N(如圖),求證:四邊形OMBN的面積為一個(gè)定值,并求出這個(gè)定值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
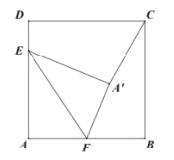
【題目】如圖,在邊長(zhǎng)為![]() 的正方形
的正方形![]() 中,點(diǎn)
中,點(diǎn)![]() 為
為![]() 的靠近點(diǎn)
的靠近點(diǎn)![]() 的四等分點(diǎn),點(diǎn)
的四等分點(diǎn),點(diǎn)![]() 為
為![]() 的中點(diǎn), 將
的中點(diǎn), 將![]() 沿著
沿著![]() 翻折得
翻折得![]() ,連接
,連接![]() ,則點(diǎn)
,則點(diǎn)![]() 到
到![]() 的距離為( )
的距離為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校九年級(jí)(1)班全體學(xué)生2018年初中畢業(yè)體育學(xué)業(yè)考試成績(jī)統(tǒng)計(jì)表如下:
成績(jī)/分 | 45 | 49 | 52 | 54 | 55 | 58 | 60 |
人數(shù) | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根據(jù)上表中信息判斷,下列結(jié)論中錯(cuò)誤的是( )
A.該班一共有40名同學(xué)
B.該班學(xué)生這次考試成績(jī)的眾數(shù)是55分
C.該班學(xué)生這次考試成績(jī)的中位數(shù)是55分
D.該班學(xué)生這次考試成績(jī)的平均數(shù)是55分
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
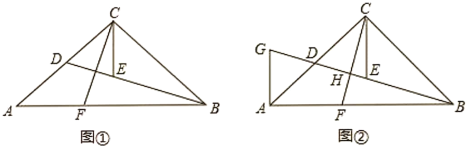
【題目】如圖①,在![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 平分
平分![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 上,且
上,且![]()
(1)求證:![]()
(2)如圖②,過點(diǎn)![]() 作
作![]() 交
交![]() 的延長(zhǎng)線于點(diǎn)
的延長(zhǎng)線于點(diǎn)![]()
①若![]() ,求
,求![]()
②設(shè)![]() 交
交![]() 于
于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四邊形![]() 中,
中,![]() 為一條對(duì)角線,
為一條對(duì)角線,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() .
.
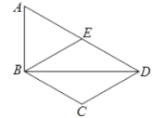
(1)求證:四邊形![]() 為菱形;
為菱形;
(2)連接![]() ,若
,若![]() 平分
平分![]() ,
,![]() ,求
,求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,點(diǎn)A(x1,y1),B(x2,y2),若x1x2+y1y2=0,且A,B均不為原點(diǎn),則稱A和B互為正交點(diǎn).比如:A(1,1),B(2,﹣2),其中1×2+1×(﹣2)=0,那么A和B互為正交點(diǎn).
(1)點(diǎn)P和Q互為正交點(diǎn),P的坐標(biāo)為(﹣2,3),
①如果Q的坐標(biāo)為(6,m),那么m的值為多少;
②如果Q的坐標(biāo)為(x,y),求y與x之間的關(guān)系式;
(2)點(diǎn)M和N互為正交點(diǎn),直接寫出∠MON的度數(shù);
(3)點(diǎn)C,D是以(0,2)為圓心,半徑為2的圓上的正交點(diǎn),以線段CD為邊,構(gòu)造正方形CDEF,圓心F在正方形CDEF的外部,求線段OE長(zhǎng)度的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】問題背景:我們學(xué)習(xí)等邊三角形時(shí)得到直角三角形的一個(gè)性質(zhì):在直角三角形中,如果一個(gè)銳角等于30°,那么它所對(duì)的直角邊等于斜邊的一半.即:如圖1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,則:AC=![]() AB.
AB.

探究結(jié)論:小明同學(xué)對(duì)以上結(jié)論作了進(jìn)一步研究.
(1)如圖1,連接AB邊上中線CE,由于CE=![]() AB,易得結(jié)論:①△ACE為等邊三角形;②BE與CE之間的數(shù)量關(guān)系為 .
AB,易得結(jié)論:①△ACE為等邊三角形;②BE與CE之間的數(shù)量關(guān)系為 .
(2)如圖2,點(diǎn)D是邊CB上任意一點(diǎn),連接AD,作等邊△ADE,且點(diǎn)E在∠ACB的內(nèi)部,連接BE.試探究線段BE與DE之間的數(shù)量關(guān)系,寫出你的猜想并加以證明.
(3)當(dāng)點(diǎn)D為邊CB延長(zhǎng)線上任意一點(diǎn)時(shí),在(2)條件的基礎(chǔ)上,線段BE與DE之間存在怎樣的數(shù)量關(guān)系?請(qǐng)直接寫出你的結(jié)論 .
拓展應(yīng)用:如圖3,在平面直角坐標(biāo)系xOy中,點(diǎn)A的坐標(biāo)為(﹣![]() ,1),點(diǎn)B是x軸正半軸上的一動(dòng)點(diǎn),以AB為邊作等邊△ABC,當(dāng)C點(diǎn)在第一象限內(nèi),且B(2,0)時(shí),求C點(diǎn)的坐標(biāo).
,1),點(diǎn)B是x軸正半軸上的一動(dòng)點(diǎn),以AB為邊作等邊△ABC,當(dāng)C點(diǎn)在第一象限內(nèi),且B(2,0)時(shí),求C點(diǎn)的坐標(biāo).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com