
【題目】函數y=ax﹣a與y=![]() (a≠0)在同一直角坐標系中的圖象可能是( )
(a≠0)在同一直角坐標系中的圖象可能是( )
A.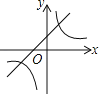 B.
B.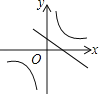
C.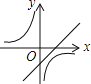 D.
D.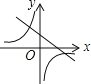
【答案】D
【解析】
當反比例函數圖象分布在第一、三象限,則a>0,然后根據一次函數圖象與系數的關系對A、B進行判斷;當反比例函數圖象分布在第二、四象限,則a<0,然后根據一次函數圖象與系數的關系對C、D進行判斷.
解:A、從反比例函數圖象得a>0,則對應的一次函數y=ax﹣a圖象經過第一、三、四象限,所以A選項錯誤;
B、從反比例函數圖象得a>0,則對應的一次函數y=ax﹣a圖象經過第一、三、四象限,所以B選項錯誤;
C、從反比例函數圖象得a<0,則對應的一次函數y=ax﹣a圖象經過第一、二、四象限,所以C選項錯誤;
D、從反比例函數圖象得a<0,則對應的一次函數y=ax﹣a圖象經過第一、二、四象限,所以D選項正確.
故選:D.


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() (1,0)和點
(1,0)和點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,對稱軸為直線
,對稱軸為直線![]() =1.
=1.
(1)求點![]() 的坐標(用含
的坐標(用含![]() 的代數式表示)
的代數式表示)
(2)連接![]() 、
、![]() ,若△
,若△![]() 的面積為6,求此拋物線的解析式;
的面積為6,求此拋物線的解析式;
(3)在(2)的條件下,點![]() 為
為![]() 軸正半軸上的一點,點
軸正半軸上的一點,點![]() 與點
與點![]() ,點
,點![]() 與點
與點![]() 關于點
關于點![]() 成中心對稱,當△
成中心對稱,當△![]() 為直角三角形時,求點
為直角三角形時,求點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明同學在查閱大數學家高斯的資料時,知道了高斯如何求1+2+3+…+100.小明于是對從1開始連續奇數的和進行了研究,發現如下式子:
第1個等式: ![]() ;第2個等式:
;第2個等式: ![]() ;第3個等式:
;第3個等式: ![]()
探索以上等式的規律,解決下列問題:
(1) ![]()
![]()
![]() ;
;
(2)完成第![]() 個等式的填空:
個等式的填空: ![]() ;
;
(3)利用上述結論,計算51+53+55+…+109 .
查看答案和解析>>
科目:初中數學 來源: 題型:
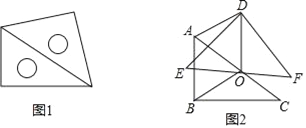
【題目】如圖1,放置的一副三角尺,將含45°角的三角尺斜邊中點O為旋轉中心,逆時針旋轉30°得到如圖2,連接OB、OD、AD.
(1)求證:△AOB≌△AOD;
(2)試判定四邊形ABOD是什么四邊形,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校組織七年級學生參加了一次“運算能力”比賽,共有400名學生參加,參賽學生的成![]() 均為正數,且最低分為60分,為了解本次比賽學生的成績分布情況,抽取了其中部分學生的成績作為樣本進行統計,并制作出了如下兩個統計圖:
均為正數,且最低分為60分,為了解本次比賽學生的成績分布情況,抽取了其中部分學生的成績作為樣本進行統計,并制作出了如下兩個統計圖:
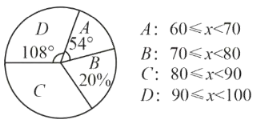
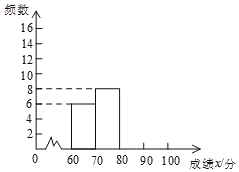
請根據所給信息,解答下列問題:
(1)所抽取分析的學生數量為 人;
(2)成績為![]() 這一組的人數占體體人數的百分比為 ;
這一組的人數占體體人數的百分比為 ;
(3)成績為![]() 這一組的所在的扇形的圓心角度數為 ;
這一組的所在的扇形的圓心角度數為 ;
(4)請補全頻數分布直方圖;
(5)若成績達到90分或以上為“優秀”等級,則參加這次比賽的學生中屬于“優秀”等級的約有 人 .
查看答案和解析>>
科目:初中數學 來源: 題型:
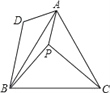
【題目】已知:如圖,在等邊△ABC中取點P,使得PA,PB,PC的長分別為3,4,5,將線段AP以點A為旋轉中心順時針旋轉60°得到線段AD,連接BD,下列結論:
①△ABD可以由△APC繞點A順時針旋轉60°得到;②點P與點D的距離為3;③∠APB=150°;
④S△APC+S△APB=![]() ,其中正確的結論有( )
,其中正確的結論有( )
A. ①②④B. ①③④C. ①②③D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠按用戶的月需求量x (件)完成一種產品的生產,其中x>0.每件的售價為18萬元,每件的成本為y (萬元),y與x的關系式為![]() (a,b為常數).經市場調研發現,月需求量x與月份n (n為整數,1≤n≤12)的關系式為x=n2-13n+72,且得到了下表中的數據.
(a,b為常數).經市場調研發現,月需求量x與月份n (n為整數,1≤n≤12)的關系式為x=n2-13n+72,且得到了下表中的數據.
月份n(月) | 1 | 2 |
成本y(萬元/件) | 11 | 12 |
(1)請直接寫出a,b的值;
(2)設第n個月的利潤為w(萬元),請求出W與n的函數關系式,并求出這一年的12個月中,哪個月份的利潤為84萬元?
(3)在這一年的前8個月中,哪個月的利潤最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com