
【題目】如圖,在邊長為![]() 的正方形
的正方形![]() 中,點
中,點![]() 為
為![]() 的靠近點
的靠近點![]() 的四等分點,點
的四等分點,點![]() 為
為![]() 的中點, 將
的中點, 將![]() 沿著
沿著![]() 翻折得
翻折得![]() ,連接
,連接![]() ,則點
,則點![]() 到
到![]() 的距離為( )
的距離為( )
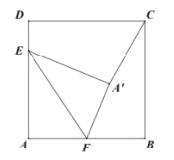
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
過點A'作GH∥AD,交AB、CD于點G、H,過點E作EK⊥GH,垂足為點K,先通過折疊可得A'E= AE=3,A'F= AF=2,∠A'=∠A=90°,再結合∠EKG=∠G=90°,證得△A'KE∽△FGA',根據相似三角形的性質可得相似比為3:2,故可設A'K=3x, FG=2x,進而表示出EK和A'G的長,再根據相似比列出方程求出x,即可求得A'G、A'H的長,再用勾股定理求得A'C的長,最后根據等積法求得點D到![]() 的距離即可.
的距離即可.
解:如圖,過點A'作GH∥AD,交AB、CD于點G、H,過點E作EK⊥GH,垂足為點K,
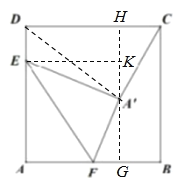
則四邊形AGKE、DEKH、BGHC均為矩形,
由題意可知DE=1,AE=3,AF=BF=2,DC=4,∠A=90°,
∵折疊,
∴A'E= AE=3,A'F= AF=2,∠A'=∠A=90°,
又∵∠EKG=∠G=90°,
∴△A'KE∽△FGA',
∴![]() ,
,
設A'K=3x,則FG=2x,
在矩形AGKE中,AE=KG=3,EK=AG=2+2x,
∴A'G=KG- A'K=3-3x
∴![]()
解得x=![]() ,
,
∴A'H=HG- A'G=4-(3-3×![]() )=
)=![]() ,
,
又∵HC=CD-DK=4-(2+2×![]() )=
)=![]() ,
,
∴在Rt△A'HC中,A'C=![]() ,
,
設點D到A'C的距離為h,
則S△A'DC=![]() A'C×h=
A'C×h=![]() CD×A'H,
CD×A'H,
∴A'C×h=CD×A'H,
∴![]() ,
,
解得h=![]() ,
,
故選:C.


科目:初中數學 來源: 題型:
【題目】(1)問題發現:如圖1,在等邊![]() 中,點
中,點![]() 為
為![]() 邊上一動點,
邊上一動點,![]() 交
交![]() 于點
于點![]() ,將
,將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 得到
得到![]() ,連接
,連接![]() .則
.則![]() 與
與![]() 的數量關系是_____,
的數量關系是_____,![]() 的度數為______.
的度數為______.
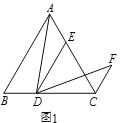
(2)拓展探究:如圖2,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為
為![]() 邊上一動點,
邊上一動點,![]() 交
交![]() 于點
于點![]() ,當∠ADF=∠ACF=90°時,求
,當∠ADF=∠ACF=90°時,求![]() 的值.
的值.
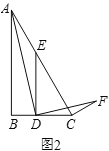
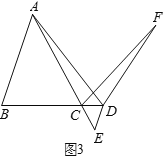
(3)解決問題:如圖3,在![]() 中,
中,![]() ,點
,點![]() 為
為![]() 的延長線上一點,過點
的延長線上一點,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,直接寫出當
,直接寫出當![]() 時
時![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在△ABC中,∠BAC=90°,AB=AC,點E在AC上(且不與點A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,連接AD,分別以AB,AD為鄰邊作平行四邊形ABFD,連接AF.
(1)請直接寫出線段AF,AE的數量關系 ;
(2)將△CED繞點C逆時針旋轉,當點E在線段BC上時,如圖②,連接AE,請判斷線段AF,AE的數量關系,并證明你的結論;
(3)在圖②的基礎上,將△CED繞點C繼續逆時針旋轉,請判斷(2)問中的結論是否發生變化?若不變,結合圖③寫出證明過程;若變化,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知函數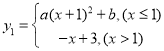 (
(![]() 為常數且
為常數且![]() ),已知當
),已知當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,請對該函數及其圖像進行如下探究:
,請對該函數及其圖像進行如下探究:

(1)求函數![]() 的解析式;
的解析式;
(2)如圖,請在平面直角坐標系中,畫出該函數的圖像;
(3)結合所畫函數圖像,請寫出該函數的一條性質;
(4)解決問題:若函數![]() 與
與![]() 至少有兩個公共點,請直接寫出
至少有兩個公共點,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為響應市政府關于“垃圾不落地![]() 市區更美麗”的主題宣傳活動,鄭州外國語中學隨機調查了部分學生對垃圾分類知識的掌握情況,調查選項分為“A:非常了解;B:比較了解;C:了解較少;D:不了解
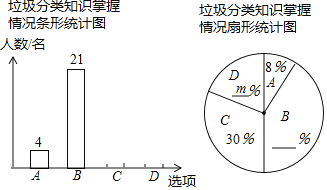
市區更美麗”的主題宣傳活動,鄭州外國語中學隨機調查了部分學生對垃圾分類知識的掌握情況,調查選項分為“A:非常了解;B:比較了解;C:了解較少;D:不了解![]() ”四種,并將調查結果繪制成以下兩幅不完整的統計圖
”四種,并將調查結果繪制成以下兩幅不完整的統計圖![]() 請根據圖中提供的信息,解答下列問題;
請根據圖中提供的信息,解答下列問題;
![]() 求
求![]() ______,并補全條形統計圖;
______,并補全條形統計圖;
![]() 若我校學生人數為1000名,根據調查結果,估計該校“非常了解”與“比較了解”的學生共有______名;
若我校學生人數為1000名,根據調查結果,估計該校“非常了解”與“比較了解”的學生共有______名;
![]() 已知“非常了解”的是3名男生和1名女生,從中隨機抽取2名向全校做垃圾分類的知識交流,請畫樹狀圖或列表的方法,求恰好抽到1男1女的概率.
已知“非常了解”的是3名男生和1名女生,從中隨機抽取2名向全校做垃圾分類的知識交流,請畫樹狀圖或列表的方法,求恰好抽到1男1女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
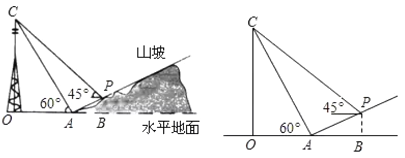
【題目】如圖,某人在山坡坡腳![]() 處測得電視塔尖點
處測得電視塔尖點![]() 的仰角為
的仰角為![]() ,沿山坡向上走到
,沿山坡向上走到![]() 處再測得點
處再測得點![]() 的仰角為
的仰角為![]() ,已知
,已知![]() 米,山坡坡度
米,山坡坡度![]() ,且
,且![]() 在同一條直線上,其中測傾器高度忽略不計.
在同一條直線上,其中測傾器高度忽略不計.
(1)求電視塔![]() 的高度;(計算結果保留根號形式)
的高度;(計算結果保留根號形式)
(2)求此人所在位置點![]() 的鉛直高度.(結果精確到0.1米,參考數據:
的鉛直高度.(結果精確到0.1米,參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
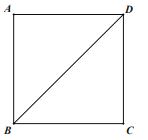
【題目】在正方形ABCD中,E是CD邊上的點,過點E作EF⊥BD于F.
(1)尺規作圖:在圖中求作點E,使得EF=EC;(保留作圖痕跡,不寫作法)
(2)在(1)的條件下,連接FC,求∠BCF的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com