
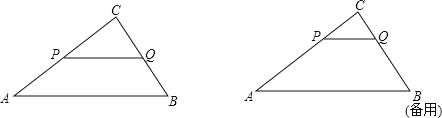
【題目】如圖:已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P點在AC上(與A、C不重合),Q在BC上.
(1)當△PQC的面積與四邊形PABQ的面積相等時,求CP的長;
(2)當△PQC的周長與四邊形PABQ的周長相等時,求CP的長;
(3)試問:在AB上是否存在一點M,使得△PQM為等腰直角三角形?若不存在,請簡要說明理由;若存在,請求出PQ的長.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 和
和![]() .
.
【解析】
(1)由于PQ∥AB,故△PQC∽△ABC,當△PQC的面積與四邊形PABQ的面積相等時,△CPQ與△CAB的面積比為1:2,根據相似三角形的面積比等于相似比的平方,可求出CP的長;
(2)由于△PQC∽△ABC,根據相似三角形的性質,可用CP表示出PQ和CQ的長,進而可表示出AP、BQ的長.根據△CPQ和四邊形ABQP的周長相等,可將相關的各邊相加,即可求出CP的長;
(3)因為不能確定哪個角是直角,故應分類討論.
①當∠MPQ=90°,且PM=PQ時.因為△CPQ∽△CAB,根據相似三角形邊長的比等于高的比,可求出PQ的值;
②∠PQM=90°時與①相同;
③當∠PMQ=90°,且PM=MQ時,過M作ME⊥PQ,則ME=![]() PQ,根據相似三角形邊長的比等于高的比,可求出PQ的值.
PQ,根據相似三角形邊長的比等于高的比,可求出PQ的值.
(1)∵PQ∥AB,
∴△PQC∽△ABC,
∵S△PQC=S四邊形PABQ,
∴S△PQC:S△ABC=1:2,
∴![]() ,
,
∴CP=![]() CA=2
CA=2![]() ;
;
(2)∵△PQC∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴CQ=![]() CP,
CP,
同理:PQ=![]() CP,
CP,
∴l△PCQ=CP+PQ+CQ=CP+![]() CP+
CP+![]() CP=3CP,
CP=3CP,
I四邊形PABQ=PA+AB+BQ+PQ,
=4﹣CP+AB+3﹣CQ+PQ,
=4﹣CP+5+3﹣![]() CP+
CP+![]() CP,
CP,
=12﹣![]() CP,
CP,
∴12﹣![]() CP=3CP,
CP=3CP,
∴![]() CP=12,
CP=12,
∴CP=![]() ;
;
(3)∵AC=4,AB=5,BC=3,
∴△ABC中AB邊上的高為![]() ,
,
①當∠MPQ=90°,且PM=PQ時,
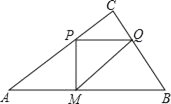
∵△CPQ∽△CAB,
∴![]() ,
,
∴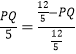 ,
,
∴PQ=![]() ;
;
②當∠PQM=90°時與①相同;
③當∠PMQ=90°,且PM=MQ時,
過M作ME⊥PQ,則ME=![]() PQ,
PQ,
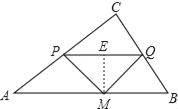
∴△CPQ的高為![]() ﹣ME=
﹣ME=![]() ﹣
﹣![]() PQ,
PQ,
∴![]() ,
,
∴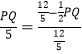 ,
,
∴PQ=![]() .
.
綜合①②③可知:點M存在,PQ的長為![]() 或
或![]() .
.


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:初中數學 來源: 題型:
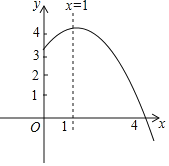
【題目】拋物線![]() 的部分圖象如圖所示,與x軸的一個交點坐標為
的部分圖象如圖所示,與x軸的一個交點坐標為![]() ,拋物線的對稱軸是
,拋物線的對稱軸是![]() 下列結論中:
下列結論中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有兩個不相等的實數根;
有兩個不相等的實數根;![]() 拋物線與x軸的另一個交點坐標為
拋物線與x軸的另一個交點坐標為![]() ;
;![]() 若點
若點![]() 在該拋物線上,則
在該拋物線上,則![]() .
.
其中正確的有![]()
![]()
A. 5個 B. 4個 C. 3個 D. 2個
查看答案和解析>>
科目:初中數學 來源: 題型:
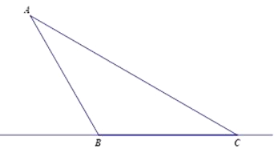
【題目】為保證車輛行駛安全,現在公路旁設立一檢測點A觀測行駛的汽車是否超速.如圖,檢測點A到公路的距離是24米,在公路上取兩點B、C,使得∠ACB=30°,∠ABC=120°.
(1)求BC的長(結果保留根號);
(2)已知該路段限速為45千米/小時,若測得某汽車從B到C用時2秒,這輛汽車是否超速?說明理由.(參考數據:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中數學 來源: 題型:
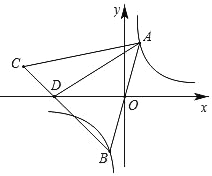
【題目】如圖,已知點A是反比例函數y=![]() 的圖象在第一象限上的動點,連結AO并延長交另一分支于點B,以AB為邊作等邊△ABC使點C落在第二象限,且邊BC交x軸于點D,若△ACD與△ABD的面積之比為1:2,則點C的坐標為__.
的圖象在第一象限上的動點,連結AO并延長交另一分支于點B,以AB為邊作等邊△ABC使點C落在第二象限,且邊BC交x軸于點D,若△ACD與△ABD的面積之比為1:2,則點C的坐標為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將邊長為2cm的正方形ABCD沿其對角線AC剪開,再把△ABC沿著AD方向平移,得到△A′B′C′,若兩個三角形重疊部分的面積為1cm2,則它移動的距離AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
查看答案和解析>>
科目:初中數學 來源: 題型:
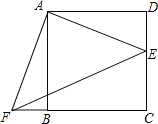
【題目】如圖,點E是正方形ABCD的邊DC上一點,把△ADE順時針旋轉△ABF的位置.
(1)旋轉中心是點 ,旋轉角度是 度;
(2)若連結EF,則△AEF是 三角形;并證明;
(3)若四邊形AECF的面積為25,DE=2,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
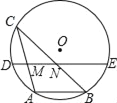
【題目】如圖,⊙O的弦AB=4cm,點C為優弧![]() 上的動點,且∠ACB=30°.若弦DE經過弦AC、BC的中點M、N,則DM+EN的最大值是_____cm.
上的動點,且∠ACB=30°.若弦DE經過弦AC、BC的中點M、N,則DM+EN的最大值是_____cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
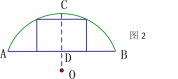
【題目】如圖,某地有一座圓弧形拱橋,
(1)如圖1,請用尺規作出圓弧所在圓的圓心O;
![]()
(2)如圖2,過點O作OC⊥AB于點D,交圓弧于點C,CD=2.4 m.橋下水面寬度AB為7.2 m,現有一艘寬3 m、船艙頂部為方形并高出水面2 m的貨船要經過拱橋,請通過計算說明此貨船能否順利通過這座拱橋.
查看答案和解析>>
科目:初中數學 來源: 題型:
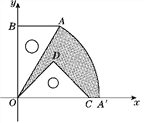
【題目】如圖,有一塊含30°角的直角三角板OAB的直角邊BO的長恰與另一塊等腰直角三角板ODC的斜邊OC的長相等,把這兩塊三角板放置在平面直角坐標系中,且OB=3![]() .
.
(1)若某反比例函數的圖象的一個分支恰好經過點A,求這個反比例函數的解析式;
(2)若把含30°角的直角三角板繞點O按順時針方向旋轉后,斜邊OA恰好落在x軸上,點A落在點A′處,試求圖中陰影部分的面積.(結果保留π)
【答案】(1)反比例函數的解析式為y=![]() ;(2)S陰影=6π-
;(2)S陰影=6π-![]() .
.
【解析】分析:(1)根據tan30°=![]() ,求出AB,進而求出OA,得出A的坐標,設過A的雙曲線的解析式是y=
,求出AB,進而求出OA,得出A的坐標,設過A的雙曲線的解析式是y=![]() ,把A的坐標代入求出即可;(2)求出∠AOA′,根據扇形的面積公式求出扇形AOA′的面積,求出OD、DC長,求出△ODC的面積,相減即可求出答案.
,把A的坐標代入求出即可;(2)求出∠AOA′,根據扇形的面積公式求出扇形AOA′的面積,求出OD、DC長,求出△ODC的面積,相減即可求出答案.
本題解析:
(1)在Rt△OBA中,∠AOB=30°,OB=3![]() ,
,
∴AB=OB·tan 30°=3.
∴點A的坐標為(3,3![]() ).
).
設反比例函數的解析式為y=![]() (k≠0),
(k≠0),
∴3![]() =
=![]() ,∴k=9
,∴k=9![]() ,則這個反比例函數的解析式為y=
,則這個反比例函數的解析式為y=![]() .
.
(2)在Rt△OBA中,∠AOB=30°,AB=3,
sin ∠AOB=![]() ,即sin 30°=
,即sin 30°=![]() ,
,
∴OA=6.
由題意得:∠AOC=60°,S扇形AOA′=![]() =6π.
=6π.
在Rt△OCD中,∠DOC=45°,OC=OB=3![]() ,
,
∴OD=OC·cos 45°=3![]() ×
×![]() =
=![]() .
.
∴S△ODC=![]() OD2=
OD2=![]()
![]() =
=![]() .
.
∴S陰影=S扇形AOA′-S△ODC=6π-![]() .
.
點睛:本題考查了勾股定理、待定系數法求函數解析式、特殊角的三角函數值、扇形的面積及等腰三角形的性質,本題屬于中檔題,難度不大,將不規則的圖形的面積表示成多個規則圖形的面積之和是解答本題的關鍵.
【題型】解答題
【結束】
26
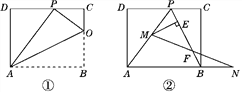
【題目】矩形ABCD一條邊AD=8,將矩形ABCD折疊,使得點B落在CD邊上的點P處.
(1)如圖①,已知折痕與邊BC交于點O,連接AP,OP,OA.
① 求證:△OCP∽△PDA;
② 若△OCP與△PDA的面積比為1:4,求邊AB的長.
(2)如圖②,在(1)的條件下,擦去AO和OP,連接BP.動點M在線段AP上(不與點P,A重合),動點N在線段AB的延長線上,且BN=PM,連接MN交PB于點F,作ME⊥BP于點E.試問動點M,N在移動的過程中,線段EF的長度是否發生變化?若不變,求出線段EF的長度;若變化,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com