
【題目】從一副52張(沒有大小王)的撲克中,每次抽出1張,然后放回洗勻再抽,在實驗中得到下列表中部分數據:
實驗次數 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
出現方塊的次數 | 11 | 18 | a | 40 | 49 | 63 | 68 | 80 | 91 | 100 |
出現方塊的頻率 | 27.5% | 22.5% | 25% | 25% | 24.5% | 26.25% | 24.3% | b | 25% | 25% |
(1)填空a= ,b= ;
(2)從上面的圖表中可以估計出現方塊的概率是 ;
(3)將這幅撲克中的所有方塊(即從方塊1到方塊13,共13張)取出,將它們背面朝上重新洗牌后,從中摸出一張,若摸出的這張牌面數字為奇數,則甲方贏,若摸出的這張牌的牌面數字是偶數,則乙方贏,你認為這個游戲對雙方是公平的嗎說明理由.
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,∠B<90,BC>AB.作AE⊥BC于點E,AF⊥CD于點F,記∠EAF的度數為α,AE=a,AF=b.則以下選項錯誤的是( )

A. ∠D的度數為α
B. a∶b=CD∶BC
C. 若α=60,則平行四邊形ABCD的周長為 ![]()
D. 若α=60,則四邊形AECF的面積為平行四邊形ABCD面積的一半
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,OC是∠AOB內一條射線,OD、OE分別是∠AOC、∠BOC的平分線.
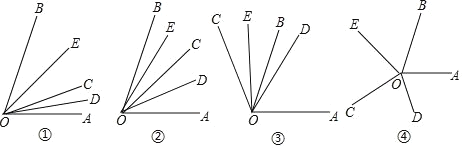
(1)如圖①,當∠AOB=80°時,∠DOE=_______°;
(2)如圖②,當射線OC在∠AOB內繞O點旋轉時,∠BOE、∠EOD、∠DOA三角之間有怎樣的數量關系?并說明理由;
(3)當射線OC在∠AOB外如圖③所示位置時,(2)中三個角:∠BOE、∠EOD、∠DOA之間數量關系是_______;
(4)當射線OC在∠AOB外如圖④所示位置時,∠BOE、∠EOD、∠DOA之間數量關系是_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AD為△ABC的高,AD=BC,以AB為底邊作等腰Rt△ABE,EF∥AD,交AC于F,連ED,EC,有以下結論:①△ADE≌△BCE;②CE⊥AB;③BD=2EF;④S△BDE=S△ACE,其中正確的是( )

A.①②③B.②④C.①③D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的材料:
按照一定順序排列著的一列數稱為數列,數列中的每一個數叫做這個數列的項.排在第一位的數稱為第一項,記為a1,排在第二位的數稱為第二項,記為a2,以此類推,排在第n位的數稱為第n項,記為![]() .所以,數列的一般形式可以寫成:
.所以,數列的一般形式可以寫成:![]() ,…,
,…,![]() ,…,一般的,如果一個數列從第二項起,每一項與它前一項的差等于同一個常數,那么這個數列叫做等差數列,這個常數叫做等差數列公差,公差通常用d表示.如:數列1,3,5,7,…為等差數列,期中a1=1,a2=3,公差為d=2.根據以上材料,解答下列問題:
,…,一般的,如果一個數列從第二項起,每一項與它前一項的差等于同一個常數,那么這個數列叫做等差數列,這個常數叫做等差數列公差,公差通常用d表示.如:數列1,3,5,7,…為等差數列,期中a1=1,a2=3,公差為d=2.根據以上材料,解答下列問題:
(1)等差數列5,10,15,…的公差d為 ,第5項是 .
(2)如果一個數列![]() ,…,
,…,![]() ,…,是等差數列,且公差為d,那么根據定義可得到:
,…,是等差數列,且公差為d,那么根據定義可得到:![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,….所以
,….所以
![]()
![]()
![]()
……由此,請你填空完成等差數列的通項公式:![]() ( )d
( )d
(3)求-4039是等差數列-5,-7,-9,…的第幾項?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
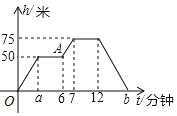
【題目】某次大型活動,組委會啟用無人機航拍活動過程,在操控無人機時應根據現場狀況調節高度,已知無人機在上升和下降過程中速度相同,設無人機的飛行高度h(米)與操控無人機的時間t(分鐘)之間的關系如圖中的實線所示,根據圖象回答下列問題:
(1)圖中的自變量是______,因變量是______;
(2)無人機在75米高的上空停留的時間是______分鐘;
(3)在上升或下降過程中,無人機的速度______為米/分;
(4)圖中a表示的數是______;b表示的數是______;
(5)圖中點A表示______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】工匠制作某種金屬工具要進行材料煅燒和鍛造兩個工序,即需要將材料燒到800℃,然后停止煅燒進行鍛造操作,經過8min時,材料溫度降為600℃.煅燒時溫度y(℃)與時間x(min)成一次函數關系;鍛造時,溫度y(℃)與時間x(min)成反比例函數關系(如圖).已知該材料初始溫度是32℃.

(1)分別求出材料煅燒和鍛造時y與x的函數關系式,并且寫出自變量x的取值范圍;
(2)根據工藝要求,當材料溫度低于480℃時,須停止操作.那么鍛造的操作時間有多長?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】結合數軸與絕對值的知識回答下列問題:
(1)數軸上表示4和1的兩點之間的距離是 ;表示-3和2兩點之間的距離是 ;一般地,數軸上表示數m和數n的兩點之間的距離等于|m-n|.
(2)如果|x+1|=3,那么x= ;
(3)若|a-3|=2,|b+2|=1,且數a、b在數軸上表示的數分別是點A、點B,則A、B 兩點間的最大距離是 .
(4)若數軸上表示a的點位于-4與2之間,則|a+4|+|a-2= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com