
【題目】閱讀下面的文字,解答問題:大家知道![]() 是無理數,而無理數是無限不循環小數,因此
是無理數,而無理數是無限不循環小數,因此![]() 的小數部分我們不可能全部地寫出來,但是由于1<
的小數部分我們不可能全部地寫出來,但是由于1<![]() <2,所以
<2,所以![]() 的整數部分為1,將
的整數部分為1,將![]() 減去其整數部分1,差就是小數部分
減去其整數部分1,差就是小數部分![]() ,根據以上的內容,解答下面的問題:
,根據以上的內容,解答下面的問題:
(1)![]() 的整數部分是______,小數部分是______;
的整數部分是______,小數部分是______;
(2)![]() 的整數部分是______,小數部分是_____;
的整數部分是______,小數部分是_____;
(3)若設![]() 整數部分是x,小數部分是y,求x﹣
整數部分是x,小數部分是y,求x﹣![]() y的值.
y的值.
科目:初中數學 來源: 題型:
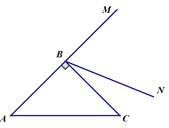
【題目】如圖,BN是等腰Rt△ABC的外角∠CBM內部的一條射線,∠ABC=90°,AB=CB,點C關于BN的對稱點為D,連接AD,BD,CD,其中CD,AD分別交射線BN于點E,P.
(1)依題意補全圖形;
(2)若∠CBN=![]() ,求∠BDA的大小(用含
,求∠BDA的大小(用含![]() 的式子表示);
的式子表示);
(3)用等式表示線段PB,PA與PE之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(8分)如圖,已知直線y=x+k和雙曲線y=![]() (k為正整數)交于A,B兩點.
(k為正整數)交于A,B兩點.
(1)當k=1時,求A、B兩點的坐標;
(2)當k=2時,求△AOB的面積;
(3)當k=1時,△OAB的面積記為S1,當k=2時,△OAB的面積記為S2,…,依此類推,當k=n時,△OAB的面積記為Sn,若S1+S2+…+Sn=![]() ,求n的值.
,求n的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一艘海輪在A點時測得燈塔C在它的北偏東42°方向上,它沿正東方向航行80海里后到達B處,此時燈塔C在它的北偏西55°方向上.
(1)求海輪在航行過程中與燈塔C的最短距離(結果精確到0.1);
(2)求海輪在B處時與燈塔C的距離(結果保留整數).
(參考數據:sin55°≈0.819,cos55°≈0.574,tan55°≈1.428,tan42°≈0.900,tan35°≈0.700,tan48°≈1.111)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 朗讀者
朗讀者![]() 自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級
自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級![]() 、
、![]() 班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績
班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績![]() 滿分為100分
滿分為100分![]() 如圖所示.
如圖所示.
平均數 | 中位數 | 眾數 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根據圖示填寫表格;
根據圖示填寫表格;
![]() 結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
![]() 如果規定成績較穩定班級勝出,你認為哪個班級能勝出?說明理由.
如果規定成績較穩定班級勝出,你認為哪個班級能勝出?說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 的對角線
的對角線![]() 與
與![]() 相交于點E,點G為
相交于點E,點G為![]() 的中點,連接
的中點,連接![]() ,
,![]() 的延長線交
的延長線交![]() 的延長線于點F,連接
的延長線于點F,連接![]() .
.
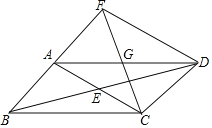
(1)求證:![]() ;
;
(2)若![]() ,
,![]() ,判斷四邊形
,判斷四邊形![]() 的形狀,并證明你的結論.
的形狀,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD和正方形OPEF中,邊AD與邊OP重合,![]() ,
,![]() ,點M、N分別在正方形ABCD的邊BC、CD上,且
,點M、N分別在正方形ABCD的邊BC、CD上,且![]() .將正方形OPEF以每秒2個單位的速度向右平移,當點F與點B重合時,停止平移.設平移時間為t秒.
.將正方形OPEF以每秒2個單位的速度向右平移,當點F與點B重合時,停止平移.設平移時間為t秒.
(1)請求出t的取值范圍;
(2)猜想:正方形OPEF的平移過程中,OE與NM的位置關系.并說明理由.
(3)連結DE、BE.當![]() 的面積等于7時,試求出正方形OPEF的平移時間t的值.
的面積等于7時,試求出正方形OPEF的平移時間t的值.


備用圖
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數y=kx+b的圖象經過點A(﹣2,6),且與x軸相交于點B,與y軸交于點D,與正比例函數y=3x的圖象相交于點C,點C的橫坐標為1.

(1)求k,b的值;
(2)請直接寫出不等式kx+b﹣3x>0的解集;
(3)M為射線CB上一點,過點M作y軸的平行線交y=3x于點N,當MN=OD時,求M點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
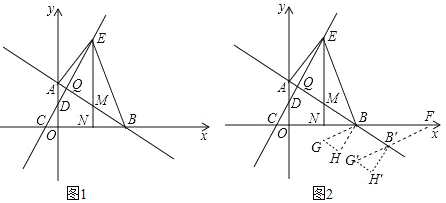
【題目】如圖1,在平面直角坐標系中,直線AB與y軸交于點![]() ,與x軸交于點B,
,與x軸交于點B,![]() ,直線CD與y軸交于點D,與x軸交于點
,直線CD與y軸交于點D,與x軸交于點![]() ,
,![]() ,直線AB與直線CD交于點Q,E為直線CD上一動點,過點E作x軸的垂線,交直線AB于點M,交x軸于點N,連接AE、BE.
,直線AB與直線CD交于點Q,E為直線CD上一動點,過點E作x軸的垂線,交直線AB于點M,交x軸于點N,連接AE、BE.
![]() 求直線AB、CD的解析式及點Q的坐標;
求直線AB、CD的解析式及點Q的坐標;
![]() 當E點運動到Q點的右側,且
當E點運動到Q點的右側,且![]() 的面積為
的面積為![]() 時,在y軸上有一動點P,直線AB上有一動點R,當
時,在y軸上有一動點P,直線AB上有一動點R,當![]() 的周長最小時,求點P的坐標及
的周長最小時,求點P的坐標及![]() 周長的最小值.
周長的最小值.
![]() 在
在![]() 問的條件下,如圖2將
問的條件下,如圖2將![]() 繞著點B逆時針旋轉
繞著點B逆時針旋轉![]() 得到
得到![]() ,使點M與點G重合,點N與點H重合,再將
,使點M與點G重合,點N與點H重合,再將![]() 沿著直線AB平移,記平移中的
沿著直線AB平移,記平移中的![]() 為
為![]() ,在平移過程中,設直線
,在平移過程中,設直線![]() 與x軸交于點F,是否存在這樣的點F,使得
與x軸交于點F,是否存在這樣的點F,使得![]() 為等腰三角形?若存在,求出此時點F的坐標;若不存在,說明理由
為等腰三角形?若存在,求出此時點F的坐標;若不存在,說明理由
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com