
【題目】(材料閱讀)數(shù)軸是數(shù)學(xué)學(xué)習(xí)的一個(gè)很重要的工具,利用數(shù)軸可以將數(shù)與形完美結(jié)合.通過數(shù)軸我們可發(fā)現(xiàn)許多重要的規(guī)律:
①對(duì)值的幾何意義:一般地,若點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() 在數(shù)軸上表示的有理數(shù)分別為
在數(shù)軸上表示的有理數(shù)分別為![]() ,
,![]() ,那么
,那么![]() 、
、![]() 兩點(diǎn)之間的距離表示為
兩點(diǎn)之間的距離表示為![]() ,記作
,記作![]() ,
,![]() 則表示數(shù)
則表示數(shù)![]() 和1在數(shù)軸上對(duì)應(yīng)的兩點(diǎn)之間的距離;又如
和1在數(shù)軸上對(duì)應(yīng)的兩點(diǎn)之間的距離;又如![]() ,所以
,所以![]() 表示數(shù)
表示數(shù)![]() 和
和![]() 在數(shù)軸上對(duì)應(yīng)的兩點(diǎn)之間的距離;
在數(shù)軸上對(duì)應(yīng)的兩點(diǎn)之間的距離;
②若數(shù)軸上點(diǎn)![]() 、點(diǎn)
、點(diǎn)![]() 表示的數(shù)分別為
表示的數(shù)分別為![]() 、
、![]() ,那么線段
,那么線段![]() 的中點(diǎn)
的中點(diǎn)![]() 表示的數(shù)為
表示的數(shù)為![]() .
.
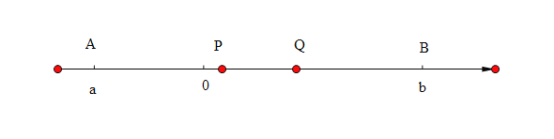
(問題情境)如圖,在數(shù)軸上,點(diǎn)![]() 表示的數(shù)為
表示的數(shù)為![]() ,點(diǎn)
,點(diǎn)![]() 在原點(diǎn)右側(cè),表示的數(shù)為
在原點(diǎn)右側(cè),表示的數(shù)為![]() ,動(dòng)點(diǎn)
,動(dòng)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)以每秒
出發(fā)以每秒![]() 個(gè)單位長度的速度沿?cái)?shù)軸正方向運(yùn)動(dòng),同時(shí),動(dòng)點(diǎn)
個(gè)單位長度的速度沿?cái)?shù)軸正方向運(yùn)動(dòng),同時(shí),動(dòng)點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)以每秒
出發(fā)以每秒![]() 個(gè)單位長度的速度沿?cái)?shù)軸負(fù)方向運(yùn)動(dòng),其中線段
個(gè)單位長度的速度沿?cái)?shù)軸負(fù)方向運(yùn)動(dòng),其中線段![]() 的中點(diǎn)記作點(diǎn)
的中點(diǎn)記作點(diǎn)![]() .
.
![]()
(綜合運(yùn)用)
(1)出發(fā)![]() 秒后,點(diǎn)
秒后,點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 相遇,則
相遇,則![]() 表示的數(shù)
表示的數(shù)![]() ___________;
___________;
(2)在第(1)問的基礎(chǔ)上,當(dāng)![]() 時(shí),求運(yùn)動(dòng)時(shí)間;
時(shí),求運(yùn)動(dòng)時(shí)間;
(3)在第(1)問的基礎(chǔ)上,點(diǎn)![]() 、
、![]() 在相遇后繼續(xù)以原來的速度在這條數(shù)軸上運(yùn)動(dòng),但
在相遇后繼續(xù)以原來的速度在這條數(shù)軸上運(yùn)動(dòng),但![]() 、
、![]() 兩點(diǎn)運(yùn)動(dòng)的方向相同.隨著點(diǎn)
兩點(diǎn)運(yùn)動(dòng)的方向相同.隨著點(diǎn)![]() 、
、![]() 的運(yùn)動(dòng),線段
的運(yùn)動(dòng),線段![]() 的中點(diǎn)
的中點(diǎn)![]() 也相應(yīng)移動(dòng),問線段
也相應(yīng)移動(dòng),問線段![]() 的中點(diǎn)
的中點(diǎn)![]() 能否與表示
能否與表示![]() 的點(diǎn)重合?若能,求出從
的點(diǎn)重合?若能,求出從![]() 、
、![]() 相遇起經(jīng)過的運(yùn)動(dòng)時(shí)間;若不能,請(qǐng)說明理由.
相遇起經(jīng)過的運(yùn)動(dòng)時(shí)間;若不能,請(qǐng)說明理由.
【答案】(1)![]() ;
;
(2)8秒或者16秒;
(3)![]() 能與表示
能與表示![]() 的點(diǎn)重合,
的點(diǎn)重合,![]() 秒.
秒.
【解析】
(1)根據(jù)題意即可得到結(jié)論;
(2)由(1)可知點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 在點(diǎn)A與B上運(yùn)動(dòng)時(shí)相遇的時(shí)間是12秒,求出
在點(diǎn)A與B上運(yùn)動(dòng)時(shí)相遇的時(shí)間是12秒,求出![]() 、
、![]() 兩點(diǎn)在
兩點(diǎn)在![]() 上運(yùn)動(dòng),相遇的時(shí)間
上運(yùn)動(dòng),相遇的時(shí)間![]() ,則可以利用兩個(gè)相遇時(shí)間的差,得出沒相遇時(shí),滿足
,則可以利用兩個(gè)相遇時(shí)間的差,得出沒相遇時(shí),滿足![]() 的時(shí)間,或者利用兩個(gè)相遇時(shí)間的和,得出相遇后,點(diǎn)
的時(shí)間,或者利用兩個(gè)相遇時(shí)間的和,得出相遇后,點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 繼續(xù)運(yùn)動(dòng),滿足
繼續(xù)運(yùn)動(dòng),滿足![]() 時(shí)的時(shí)間;
時(shí)的時(shí)間;
(3)當(dāng)線段![]() 的中點(diǎn)
的中點(diǎn)![]() 與表示
與表示![]() 的點(diǎn)重合時(shí),點(diǎn)
的點(diǎn)重合時(shí),點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 向數(shù)軸的負(fù)方向運(yùn)動(dòng),設(shè)點(diǎn)
向數(shù)軸的負(fù)方向運(yùn)動(dòng),設(shè)點(diǎn)![]() 表示的數(shù)是x,點(diǎn)
表示的數(shù)是x,點(diǎn)![]() 表示的數(shù)是y,由此可得
表示的數(shù)是y,由此可得![]() ,并根據(jù)中點(diǎn)的數(shù)的表示公式
,并根據(jù)中點(diǎn)的數(shù)的表示公式![]() ,化簡(jiǎn)求值即可.
,化簡(jiǎn)求值即可.
解:(1)依題意得:![]() ,并且
,并且![]() ,
,
則有![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
(2)
如圖示:
∵![]()
∴設(shè)![]() 、
、![]() 兩點(diǎn)在
兩點(diǎn)在![]() 上運(yùn)動(dòng),相遇的時(shí)間是
上運(yùn)動(dòng),相遇的時(shí)間是![]() ,則,
,則,
依題意得:![]() ,
,
解之得:![]() ,
,
由(1)可知,在![]() 上出發(fā)
上出發(fā)![]() 秒后,點(diǎn)
秒后,點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 相遇,
相遇,
∴當(dāng)點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 沒相遇時(shí),使
沒相遇時(shí),使![]() ,
,
時(shí)間為:![]() ,
,
當(dāng)點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 相遇又分開時(shí),使
相遇又分開時(shí),使![]() ,
,
時(shí)間為:![]() ,
,
即:出發(fā)8秒或者16秒后,![]() ,
,
(3)![]() 能與表示
能與表示![]() 的點(diǎn)重合,
的點(diǎn)重合,
線段![]() 的中點(diǎn)
的中點(diǎn)![]() 與表示
與表示![]() 的點(diǎn)重合時(shí),點(diǎn)
的點(diǎn)重合時(shí),點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 向數(shù)軸的負(fù)方向運(yùn)動(dòng),
向數(shù)軸的負(fù)方向運(yùn)動(dòng),
如圖示:

點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 在C點(diǎn)相遇,
在C點(diǎn)相遇,
∴![]() ,
,
∴點(diǎn)C 表示的數(shù)是4,
設(shè)點(diǎn)![]() 表示的數(shù)是x,點(diǎn)
表示的數(shù)是x,點(diǎn)![]() 表示的數(shù)是y,
表示的數(shù)是y,
則依題意得:![]() ,
,
化簡(jiǎn)得:![]() ,
,
并且,根據(jù)中點(diǎn)的數(shù)的表示公式可得:![]() ,
,
即有:![]() ,代入
,代入![]() ,
,
則可得:![]() ,
,
∴![]() ,
,
∴當(dāng)線段![]() 的中點(diǎn)
的中點(diǎn)![]() 是表示
是表示![]() 的點(diǎn)時(shí),從
的點(diǎn)時(shí),從![]() 、
、![]() 相遇起經(jīng)過的運(yùn)動(dòng)時(shí)間為:
相遇起經(jīng)過的運(yùn)動(dòng)時(shí)間為:![]() (秒),
(秒),



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
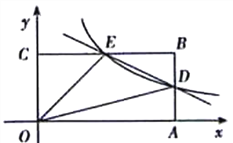
【題目】如圖,在平面直角坐標(biāo)系中,原點(diǎn)O是矩形OABC的一個(gè)頂點(diǎn),點(diǎn)A、C都
在坐標(biāo)軸上,點(diǎn)B的坐標(biāo)是(4.2),反比例函數(shù)![]() 與AB,BC分別交于點(diǎn)D,E。
與AB,BC分別交于點(diǎn)D,E。
(1)求直線DE的解析式;
(2)若點(diǎn)F為y軸上一點(diǎn),△OEF和△ODE的面積相等,求點(diǎn)F的坐標(biāo)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖是一個(gè)由5張紙片拼成的平行四邊形,相鄰紙片之間互不重疊也無縫隙,其中兩張等腰直角三角形紙片的面積都為S1,另兩張直角三角形紙片的面積都為S2,中間一張正方形紙片的面積為S3,則這個(gè)平行四邊形的面積可以表示為( )
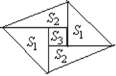
A. 4S1B. 4S2C. 4S2+S3D. 2S1+8S3
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
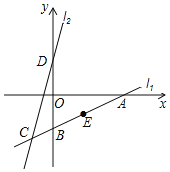
【題目】如圖,直線l1:y=![]() x-4分別與x軸,y軸交于A,B兩點(diǎn),與直線l2交于點(diǎn)C(-2,m).點(diǎn)D是直線l2與y軸的交點(diǎn),將點(diǎn)A向上平移3個(gè)單位,再向左平移8個(gè)單位恰好能與點(diǎn)D重合.
x-4分別與x軸,y軸交于A,B兩點(diǎn),與直線l2交于點(diǎn)C(-2,m).點(diǎn)D是直線l2與y軸的交點(diǎn),將點(diǎn)A向上平移3個(gè)單位,再向左平移8個(gè)單位恰好能與點(diǎn)D重合.
(1)求直線l2的解析式;
(2)已知點(diǎn)E(n,-2)是直線l1上一點(diǎn),將直線l2沿x軸向右平移.在平移過程中,當(dāng)直線l2與線段BE有交點(diǎn)時(shí),求平移距離d的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ABC=90°,點(diǎn)M是AC的中點(diǎn),以AB為直徑作⊙O分別交AC,BM于點(diǎn)D,E.
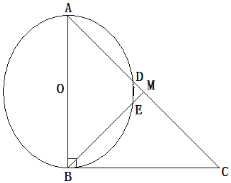
(1)求證:MD=ME
(2)填空:①若AB=6,當(dāng)AD=2DM時(shí),DE=___________;
②連接OD,OE,當(dāng)∠A的度數(shù)為____________時(shí),四邊形ODME是菱形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某游泳館普通票價(jià)20元/張,暑假為了促銷,新推出兩種優(yōu)惠卡:
①金卡售價(jià)600元/張,每次憑卡不再收費(fèi).
②銀卡售價(jià)150元/張,每次憑卡另收10元.
暑假普通票正常出售,兩種優(yōu)惠卡僅限暑假使用,不限次數(shù).設(shè)游泳x次時(shí),所需總費(fèi)用為y元.

(1)分別寫出選擇銀卡、普通票消費(fèi)時(shí),y與x之間的函數(shù)關(guān)系式;
(2)在同一坐標(biāo)系中,若三種消費(fèi)方式對(duì)應(yīng)的函數(shù)圖象如圖所示,請(qǐng)求出點(diǎn)A、B、C的坐標(biāo);
(3)請(qǐng)根據(jù)函數(shù)圖象,直接寫出選擇哪種消費(fèi)方式更合算.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
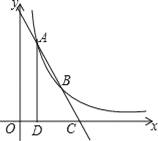
【題目】如圖,點(diǎn)A(1,4)、B(2,a)在函數(shù)y=![]() (x>0)的圖象上,直線AB與x軸相交于點(diǎn)C,AD⊥x軸于點(diǎn)D.
(x>0)的圖象上,直線AB與x軸相交于點(diǎn)C,AD⊥x軸于點(diǎn)D.
(1)m= ;
(2)求點(diǎn)C的坐標(biāo);
(3)在x軸上是否存在點(diǎn)E,使以A、B、E為頂點(diǎn)的三角形與△ACD相似?若存在,求出點(diǎn)E的坐標(biāo);若不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
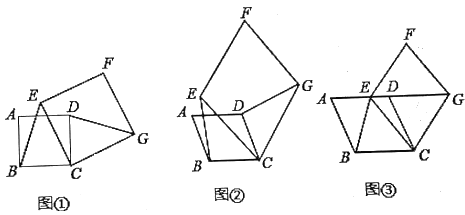
【題目】(1)(感知)如圖①,四邊形![]() 、
、![]() 均為正方形.
均為正方形.![]() 與
與![]() 的數(shù)量關(guān)系為________;
的數(shù)量關(guān)系為________;
(2)(拓展)如圖②,四邊形![]() 、
、![]() 均為菱形,且
均為菱形,且![]() .請(qǐng)判斷
.請(qǐng)判斷![]() 與
與![]() 的數(shù)量關(guān)系,并說明理由;
的數(shù)量關(guān)系,并說明理由;
(3)(應(yīng)用)如圖③,四邊形![]() 、
、![]() 均為菱形,點(diǎn)
均為菱形,點(diǎn)![]() 在邊
在邊![]() 上,點(diǎn)
上,點(diǎn)![]() 在
在![]() 延長線上.若
延長線上.若![]() ,
,![]() ,
,![]() 的面積為9,則菱形
的面積為9,則菱形![]() 的面積為_______.
的面積為_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,O為坐標(biāo)原點(diǎn),已知直線y=﹣![]() x+8與x軸、y軸分別交于A、B兩點(diǎn).直線OD⊥直線AB于點(diǎn)D.現(xiàn)有一點(diǎn)P從點(diǎn)D出發(fā),沿線段DO向點(diǎn)O運(yùn)動(dòng),另一點(diǎn)Q從點(diǎn)O出發(fā),沿線段OA向點(diǎn)A運(yùn)動(dòng),兩點(diǎn)同時(shí)出發(fā),速度都為每秒1個(gè)單位長度,當(dāng)點(diǎn)P運(yùn)動(dòng)到O時(shí),兩點(diǎn)都停止.設(shè)運(yùn)動(dòng)時(shí)間為t秒.
x+8與x軸、y軸分別交于A、B兩點(diǎn).直線OD⊥直線AB于點(diǎn)D.現(xiàn)有一點(diǎn)P從點(diǎn)D出發(fā),沿線段DO向點(diǎn)O運(yùn)動(dòng),另一點(diǎn)Q從點(diǎn)O出發(fā),沿線段OA向點(diǎn)A運(yùn)動(dòng),兩點(diǎn)同時(shí)出發(fā),速度都為每秒1個(gè)單位長度,當(dāng)點(diǎn)P運(yùn)動(dòng)到O時(shí),兩點(diǎn)都停止.設(shè)運(yùn)動(dòng)時(shí)間為t秒.
(1)點(diǎn)A的坐標(biāo)為_____;線段OD的長為_____.
(2)設(shè)△OPQ的面積為S,求S與t之間的函數(shù)關(guān)系(不要求寫出取值范圍),并確定t為何值時(shí)S的值最大?
(3)是否存在某一時(shí)刻t,使得△OPQ為等腰三角形?若存在,寫出所有滿足條件的t的值;若不存在,則說明理由.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com