【題目】已知拋物線過點A（2，0），B（﹣1，0），與y軸交于點C，且OC=2，求這條拋物線的解析式．
【答案】y=﹣x2+x+2或y=x2﹣x﹣2．
【解析】試題分析：首先由OC=2，可知C點的坐標是（0，2）或（0，-2），然后分別把A、B、C三點的坐標代入函數的解析式，用待定系數法求出．注意本題有兩種情況．
試題解析：拋物線與y軸交于點C，且OC=2，則C點的坐標是（0，2）或（0，-2），
當C點坐標是（0，2）時，圖象經過三點，可以設函數解析式是：y=ax2+bx+c，
把（2，0），（-1，0），（0，2）分別代入解析式，
得到：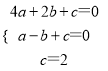 
，
解得：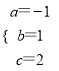 
，
則函數解析式是：y=-x2+x+2；
同理可以求得當C是（0，-2）時解析式是：y=x2-x-2．
故這條拋物線的解析式為：y=-x2+x+2或y=x2-x-2．
科目：初中數學 來源： 題型：
【題目】甲、乙兩位運動員在相同條件下各射靶10次，毎次射靶的成績情況如圖.
(1)請填寫下表:
(2)請你從平均數和方差相結合對甲、乙兩名運動員6次射靶成績進行分析:
平均數 | 方差 | 中位數 | 命中9環以上的次數(包括9環) | |
甲 | 7 | 1.2 | 1 | |
乙 | 5.4 | 7.5 |
(3)教練根據兩人的成績最后選擇乙去參加比賽，你能不能說出教練讓乙去比賽的理由?(至少說出兩條理由)
查看答案和解析>>
科目：初中數學 來源： 題型：
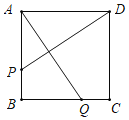
【題目】如圖，在正方形ABCD中，AB＝8厘米，如果動點P在線段AB上以2厘米/秒的速度由A點向B點運動，同時動點Q在以1厘米/秒的速度線段BC上由C點向B點運動，當點P到達B點時整個運動過程停止．設運動時間為t秒，當AQ⊥DP時，t的值為_____秒．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，BE、CD 相交于點 A，連接 BC，DE，下列條件中不能判斷△ABC∽ADE 的是（ ）
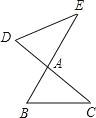
A. ∠B＝∠D B. ∠C＝∠E C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠ACB=90°，AC=6，BC=12，點D在邊BC上，點E在線段AD上，EF⊥AC于點F，EG⊥EF交AB于點G，若EF=EG，則CD的長為（ ）
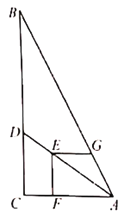
A.3.6B.4C.4.8D.5
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在邊長為6的等邊三角形ABC中，點E、F分別是邊AC、BC上的動點，連接AF、BE，交于點P，若始終保持AE=CF，當點E從點A運動到點C時，則點P運動的路徑長__________．
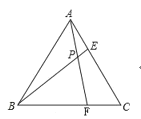
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點P從
出發，沿所示方向運動，每當碰到長方形OABC的邊時會進行反彈，反彈時反射角等于入射角，當點P第2018次碰到長方形的邊時，點P的坐標為______．
【答案】
【解析】
根據反射角與入射角的定義作出圖形；由圖可知，每6次反彈為一個循環組依次循環，用2018除以6，根據商和余數的情況確定所對應的點的坐標即可．
解：如圖所示：經過6次反彈后動點回到出發點
，
，
當點P第2018次碰到矩形的邊時為第337個循環組的第2次反彈，
點P的坐標為
．
故答案為：．
【點睛】
此題主要考查了點的坐標的規律，作出圖形，觀察出每6次反彈為一個循環組依次循環是解題的關鍵．
【題型】填空題
【結束】
15
【題目】為了保護環境，某公交公司決定購買A、B兩種型號的全新混合動力公交車共10輛，其中A種型號每輛價格為a萬元，每年節省油量為
萬升；B種型號每輛價格為b萬元，每年節省油量為
萬升：經調查，購買一輛A型車比購買一輛B型車多20萬元，購買2輛A型車比購買3輛B型車少60萬元．
請求出a和b；
若購買這批混合動力公交車每年能節省
萬升汽油，求購買這批混合動力公交車需要多少萬元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某果品超市經銷一種水果，已知該水果的進價為每千克15元，通過一段時間的銷售情況發現，該種水果每周的銷售總額相同，且每周的銷售量y（千克）與每千克售價x（元）的關系如表所示
每千克售價x（元） | 25 | 30 | 40 |
每周銷售量y（千克） | 240 | 200 | 150 |
（1）寫出每周銷售量y（千克）與每千克售價x（元）的函數關系式；
（2）由于銷售淡季即將來臨，超市要完成每周銷售量不低于300千克的任務，則該種水果每千克售價最多定為多少元？
（3）在（2）的基礎上，超市銷售該種水果能否到達每周獲利1200元？說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】Rt△ABO與Rt△CBD在平面直角坐標系中的位置如圖所示，∠ABO＝∠CBD＝90°，若點A（2
，﹣2），∠CBA＝60°，BO＝BD，則點C的坐標是（ ）
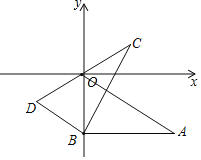
A. （2，2）B. （1，）C. （，1）D. （2，2）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com