Question

【題目】如圖,拋物線與x軸交于A(3，0)，B兩點，與y軸交于點C，點M(，5)是拋物線上一點,拋物線與拋物線關于y軸對稱,點A、B、M關于y軸的對稱點分別為點A′、B′、M′

（1）求拋物線C1的解析式；

（2）過點M′作M′E⊥x軸于點E,交直線A′C于點D,在x軸上是否存在點P,使得以A′、D. P為頂點的三角形與△AB′C相似?若存在，請求出點P的坐標；若不存在，請說明理由.

Answer 1

【答案】（1） （2）P(2,0)或(,0)

【解析】(1)、將點A和點M的坐標代入，利用待定系數法求出函數解析式；(2)、根據函數解析式求出點B和點C的坐標，然后利用軸對稱性得出點M′、點A′和點B′的坐標，從而得出直線A′C的直線解析式，根據勾股定理分別求出AC和DA′的長度，設P（m，0），分和兩種情況分別求出m的值，得出點P的坐標．

(1)、把A（-3，0），M（，5）代入y=ax2+bx+4得：，

解得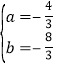：， 所以拋物線C1的解析式為，

(2)、令y=0，則， 解得x1=-3，x2=1， ∴B（1，0），
令x=0，則y=4，∴C（0，4）．由題意，知M′（，5），B′（-1，0），A′（3，0），∠CAA′=∠CA′A，∴AB′=2．設直線A′C的解析式為y=px+q．

把A′（3，0），C（0，4）代入得：，解得：，∴y=，

當x=時，y==2，∴D(，2） 由勾股定理得，AC=5， DA′=．

設P（m，0）． 當m＜3時，此時點P在點A′的左邊， 若，即有△DA′P∽△CAB′，

∴， 解得m=2， ∴P（2，0）；

若，即有△DA′P∽△B′AC，∴， 解得m=，∴P(，0)；

當m＞3時，此時點P在點A′的右邊，∵∠CB′O≠∠DA′E， ∴∠AB′C≠∠DA′P，

∴此情況，△DA′P與△B′AC不能相似．

綜上所述，存在點P（2，0）或(，0)滿足條件．