
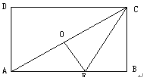
【題目】如圖,點O是矩形ABCD的中心,E是AB上的點,沿CE折疊后,點B恰好與點O重合,若BC=3,則折痕CE的長為( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 6
D. 6
科目:初中數學 來源: 題型:
【題目】“五一”期間,部分同學隨家長一同到某公園游玩,下面是購買門票時,甲同學與其爸爸的對話(如圖),試根據圖中的信息,解決下列問題:
(1)本次共去了幾個成人,幾個學生?
(2)甲同學所說的另一種購票方式,是否可以省錢?試說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校與圖書館在冋一條筆直道路上,甲從學校去圖書館,乙從圖書館回學校,甲、乙兩人都勻速步行且同時出發,乙先到達日的地.兩人之間的距離y(米)與時間t(分鐘)之間的函數關系如圖所示.
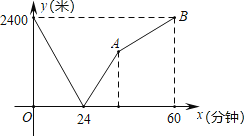
(1)根據圖象信息,當t= 分鐘時甲乙兩人相遇,乙的速度為 米/分鐘;
(2)求點A的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了發展校園足球運動,某城區五校決定聯合購買一批足球服和足球.經過市場調查發現:甲、乙兩商場以同樣的價格出售同種品牌的足球服和足球,已知每套足球服比每個足球多60元,兩套足球服與三個足球的費用相等.經洽談,甲商場的優惠方案是:每購買20套足球服,送一個足球;乙商場的優惠方案是:若購買足球服超過80套,則購買的足球打八折,若購買足球服不超過80套,不打折.
(1)求每套足球服和每個足球的價格各是多少元;
(2)若城區五校聯合購買120套足球服和![]() (
(![]() )個足球,假如你是本次購買任務的負責人,你會選擇到甲、乙兩家中的哪一家商場購買更便宜?請說明理由.
)個足球,假如你是本次購買任務的負責人,你會選擇到甲、乙兩家中的哪一家商場購買更便宜?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:若![]() ,且
,且![]() ,則我們稱
,則我們稱![]() 是
是![]() 的差余角.例如:若
的差余角.例如:若![]() ,則
,則![]() 的差余角
的差余角![]() .
.
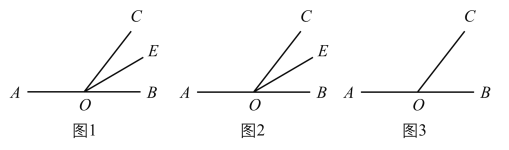
(1)如圖1,點![]() 在直線
在直線![]() 上,射線
上,射線![]() 是
是![]() 的角平分線,若
的角平分線,若![]() 是
是![]() 的差余角,求
的差余角,求![]() 的度數.
的度數.
(2)如圖2,點![]() 在直線
在直線![]() 上,若
上,若![]() 是
是![]() 的差余角,那么
的差余角,那么![]() 與
與![]() 有什么數量關系.
有什么數量關系.
(3)如圖3,點![]() 在直線
在直線![]() 上,若
上,若![]() 是
是![]() 的差余角,且
的差余角,且![]() 與
與![]() 在直線
在直線![]() 的同側,請你探究
的同側,請你探究![]() 是否為定值?若是,請求出定值;若不是,請說明理由.
是否為定值?若是,請求出定值;若不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
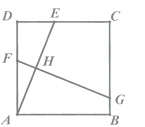
【題目】如圖,在正方形ABCD中,AD=6,點E是邊CD上的動點(點E不與端點C,D重合),AE的垂直平分線FG分別交AD,AE,BC于點F,H,G.當![]() =
=![]() 時,DE的長為( )
時,DE的長為( )
A. 2 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一副三角板中的兩塊直角三角尺的直角頂點C按如圖所示的方式疊放在一起(其中,![]() ,
,![]() ;
;![]() ).
).
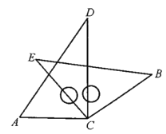
(1)①若![]() ,則
,則![]() 的度數為_____________;
的度數為_____________;
②若![]() ,則
,則![]() 的度數為_____________.
的度數為_____________.
(2)由(1)猜想![]() 與
與![]() 的數量關系,并說明理由.
的數量關系,并說明理由.
(3)當![]() 且點E在直線AC的上方時,這兩塊三角尺是否存在一組邊互相平行?若存在,請寫出
且點E在直線AC的上方時,這兩塊三角尺是否存在一組邊互相平行?若存在,請寫出![]() 角度所有可能的值(不必說明理由);若不存在,請說明理由.
角度所有可能的值(不必說明理由);若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
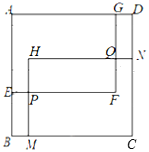
【題目】如圖,在邊長為6的正方形ABCD內部有兩個大小相同的長方形AEFG、HMCN,HM與EF相交于點P,HN與GF相交于點Q,AG=CM=x,AE=CN=y.
(1)用含有x、y的代數式表示長方形AEFG與長方形HMCN重疊部分的面積S四邊形HPFQ,并求出x應滿足的條件;
(2)當AG=AE,EF=2PE時,
①AG的長為_______;
②四邊形AEFG旋轉后能與四邊形HMCN重合,請指出該圖形所在平面內能夠作為旋轉中心的所有點,并分別說明如何旋轉的.
查看答案和解析>>
科目:初中數學 來源: 題型:
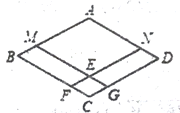
【題目】已知,四邊形ABCD是菱形,點M、N分別在AB、AD上,且BM=DN,MG∥AD,NF∥AB,點F、G分別在BC、CD上,MG與NF相交于點E;
(1)如圖,求證:四邊形AMEN是菱形;
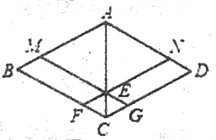
(2)如圖,連接AC,在不添加任何輔助線的情況下,請直接寫出面積相等的四邊形;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com