
【題目】七年級(1)班的全體同學排成一列步行去市博物館參加科技活動,小濤擔任通訊員.在隊伍中,小濤先數了一下他前后的人數,發現前面的人數是后面人數的2倍,他往前超了8名同學后,發現前面的人數和后面的人數一樣.
(1)七年級(1)班有多少名同學?
(2)這些同學要過一座長60米的大橋,安全起見,相鄰兩個同學間保持相同的固定距離,隊伍前進速度為1.2米/秒,從第一名同學剛上橋到全體通過大橋用了90秒,則隊伍的全長為多少米?
(3)在(2)的條件下,排在隊尾的小剛想把一則通知送到隊伍最前的小婷手中,若小剛從隊尾追趕小婷的速度是4.2米/秒,他能在15秒內追上小婷嗎?說明你的理由.
【答案】(1)七年級(1)班共有49名同學;(2)隊伍全長48米;(3)不能,理由見解析.
【解析】
(1)設七年級(1)班隊伍中小濤后面人數有x名,前面有2x名,根據題意列出方程,求出方程的解即可得到結果;
(2)設隊伍全長為y米,根據題意列出關于y的方程,求出方程的解即可得到結果;
(3)設小剛z秒追上小婷,根據題意列出關于z的方程,求出方程的解即可做出判斷.
解:(1)設小濤第一次數人數的時候他后面有![]() 名同學,則他前面有
名同學,則他前面有![]() 名同學,
名同學,
依題意,得![]() ,
,
解得![]() .
.
則![]()
![]() 七年級(1)班共有49名同學
七年級(1)班共有49名同學
(2)設隊伍全長![]() 米.
米.
依題意,得![]() ,
,
解得![]()
![]() 隊伍全長48米
隊伍全長48米
(3)不能
理由:設小剛![]() 秒追上小婷.
秒追上小婷.
依題意得:![]() ,
,
解得![]() ,
,
![]()
![]() 小剛不能在15秒內追上小婷.
小剛不能在15秒內追上小婷.
故答案為:(1)七年級(1)班共有49名同學;(2)隊伍全長48米;(3)不能,理由見解析.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,如果點A,點C為某個菱形的一組對角的頂點,且點A,C在直線y=x上,那么稱該菱形為點A,C的“極好菱形“.如圖為點A,C的“極好菱形”的一個示意圖.已知點M的坐標為(1,1),點P的坐標為(3,3).

(1)點E(2,4),F(3,2),G(4,0)中,能夠成為點M,P的“極好菱形“的頂點的是 ;
(2)若點M,P的“極好菱形”為正方形,求這個正方形另外兩個頂點的坐標;
(3)如果四邊形MNPQ是點M,P的“極好菱形”.
①當點N的坐標為(3,1)時,求四邊形MNPQ的面積;
②當四邊形MNPQ的面積為12,且與直線y=x+b有公共點時,請寫出b的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:
我們知道,![]() ,類似地,我們把
,類似地,我們把![]() 看成一個整體,則
看成一個整體,則![]()
![]() =
=![]() .“整體思想”是初中數學解題中的一種重要的思想方法,它在多項式的化簡與求職中應用極為廣泛.
.“整體思想”是初中數學解題中的一種重要的思想方法,它在多項式的化簡與求職中應用極為廣泛.
嘗試應用:
(1)把![]() 看成一個整體,合并
看成一個整體,合并![]() 的結果為_______.
的結果為_______.
(2)已知![]() ,求
,求![]() 的值.
的值.
拓廣探索:
(3)已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,∠C=90°,AC=BC=![]() ,將△ABC繞點A順時針方向旋轉60°到△AB′C′的位置,連接C′B,則C′B的長為( )
,將△ABC繞點A順時針方向旋轉60°到△AB′C′的位置,連接C′B,則C′B的長為( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
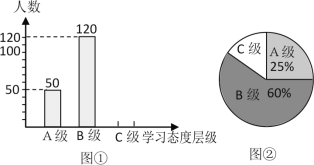
【題目】初中生對待學習的態度一直是教育工作者關注的問題之一.為此某市教育局對該市部分學校的八年級學生對待學習的態度進行了一次抽樣調查(把學習態度分為三個層級,A級:對學習很感興趣;B級:對學習較感興趣;C級:對學習不感興趣),并將調查結果繪制成圖①和圖②的統計圖(不完整).請根據圖中提供的信息,解答下列問題:
(1)此次抽樣調查中,共調查了 名學生;
(2)將圖①補充完整;
(3)求出圖②中C級所占的圓心角的度數;
(4)根據抽樣調查結果,請你估計該市近20000名初中生中大約有多少名學生學習態度達標(達標包括A級和B級)?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料,解決問題:
材料1:在研究數的整除時發現:能被5、25、125、625整除的數的特征是:分別看這個數的末一位、末兩位、末三位、末四位即可,推廣成一條結論;末![]() 位能被
位能被![]() 整除的數,本身必能被
整除的數,本身必能被![]() 整除,反過來,末
整除,反過來,末![]() 位不能被
位不能被![]() 整除的數,本身也不可能被
整除的數,本身也不可能被![]() 整除,例如判斷992250能否被25、625整除時,可按下列步驟計算:
整除,例如判斷992250能否被25、625整除時,可按下列步驟計算:
![]() ,
,![]() 為整數,
為整數,![]() 能被25整除
能被25整除
![]() ,
,![]() 不為整數,
不為整數,![]() 不能被625整除
不能被625整除
材料2:用奇偶位差法判斷一個數能否被11這個數整除時,可把這個數的奇位上的數字與偶位上的數字分別加起來,再求它們的差,看差能否被11整除,若差能被11整除,則原數能被11整除,反之則不能.
(1)若![]() 這個三位數能被11整除,則
這個三位數能被11整除,則![]() ;在該三位數末尾加上和為8的兩個數字,讓其成為一個五位數,該五位數仍能被11整除,求這個五位數
;在該三位數末尾加上和為8的兩個數字,讓其成為一個五位數,該五位數仍能被11整除,求這個五位數
(2)若一個六位數p的最高位數字為5,千位數字是個位數字的2倍,且這個數既能被125整除,又能被11整除,求這個數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上,點A和點B分別位于原點O兩側,點A對應的數為a,點B對應的數為b,且|a-b|=7
(1)若b=-3,則a的值為__________;
(2)若OA=3OB,求a的值;
(3)點C為數軸上一點,對應的數為c.若O為AC的中點,OB=3BC,求所有滿足條件的c的值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
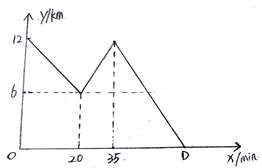
【題目】每天早晨王老師7點準時騎自行車去學校上班,今天早晨由于走的匆忙,忘帶一樣重要東西。當他騎車至距學校6千米處時,原地返回,加速回到家,取完東西又以最初出發時的速度騎車去學校。如圖是王老師今早出行的過程中他距學校的距離y(km)與他離家所用時間x(min)之間的函數圖像.
根據圖像解答下列問題:
(1)求直線AB的解析式.
(2)如果學校8:30準時上課,請問王老師能否按時到校上課?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com