
【題目】(1)(探究發現)
如圖1,![]() 的頂點
的頂點![]() 在正方形
在正方形![]() 兩條對角線的交點處,
兩條對角線的交點處,![]() ,將
,將![]() 繞點
繞點![]() 旋轉,旋轉過程中,
旋轉,旋轉過程中,![]() 的兩邊分別與正方形
的兩邊分別與正方形![]() 的邊
的邊![]() 和
和![]() 交于點
交于點![]() 和點
和點![]() (點
(點![]() 與點
與點![]() ,
,![]() 不重合).則
不重合).則![]() 之間滿足的數量關系是 .
之間滿足的數量關系是 .
(2)(類比應用)
如圖2,若將(1)中的“正方形![]() ”改為“
”改為“![]() 的菱形
的菱形![]() ”,其他條件不變,當
”,其他條件不變,當![]() 時,上述結論是否仍然成立?若成立,請給出證明;若不成立,請猜想結論并說明理由.
時,上述結論是否仍然成立?若成立,請給出證明;若不成立,請猜想結論并說明理由.
(3)(拓展延伸)
如圖3,![]() ,
,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() ,且
,且![]() ,點
,點![]() 是
是![]() 上一點,
上一點,![]() ,求
,求![]() 的長.
的長.

【答案】(1)![]() (2)結論不成立.
(2)結論不成立.![]() (3)
(3)![]()
【解析】
(1)結論:![]() .根據正方形性質,證
.根據正方形性質,證![]() ,根據全等三角形性質可得結論;(2)結論不成立.
,根據全等三角形性質可得結論;(2)結論不成立.![]() .連接
.連接![]() ,在
,在![]() 上截取
上截取![]() ,連接
,連接![]() .根據菱形性質,證
.根據菱形性質,證![]() ,
,![]() 四點共圓,分別證
四點共圓,分別證![]() 是等邊三角形,
是等邊三角形,![]() 是等邊三角形,根據等邊三角形性質證
是等邊三角形,根據等邊三角形性質證![]() ,根據全等三角形性質可得結論;(3)由
,根據全等三角形性質可得結論;(3)由![]() 可知
可知![]() 是鈍角三角形,
是鈍角三角形,![]() ,作
,作![]() 于
于![]() ,設
,設![]() .根據勾股定理,可得到
.根據勾股定理,可得到![]() ,由
,由![]() ,得
,得![]() 四點共圓,再證
四點共圓,再證![]() 是等邊三角形,由(2)可知:
是等邊三角形,由(2)可知:![]() ,故可得
,故可得![]() .
.
(1)如圖1中,結論:![]() .理由如下:
.理由如下:

∵四邊形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案為![]() .
.
(2)如圖2中,結論不成立.![]() .
.
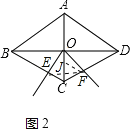
理由:連接![]() ,在
,在![]() 上截取
上截取![]() ,連接
,連接![]() .
.
∵四邊形![]() 是菱形,
是菱形,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 四點共圓,
四點共圓,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
(3)如圖3中,由![]() 可知
可知![]() 是鈍角三角形,
是鈍角三角形,![]() ,作
,作![]() 于
于![]() ,設
,設![]() .
.

在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() (舍棄)或
(舍棄)或![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 四點共圓,
四點共圓,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,
由(2)可知:![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】龍蝦狂歡季再度開啟,第![]() 屆中國合肥龍蝦節的主題是“讓你知蝦,也知稻”,稻田小龍蝦養殖技術在合肥周邊的鄉鎮大力推廣,已知每千克小龍蝦養殖成本為
屆中國合肥龍蝦節的主題是“讓你知蝦,也知稻”,稻田小龍蝦養殖技術在合肥周邊的鄉鎮大力推廣,已知每千克小龍蝦養殖成本為![]() 元,在整個銷售旺季的
元,在整個銷售旺季的![]() 天里,銷售單價
天里,銷售單價![]() 元/千克,與時間
元/千克,與時間![]() (天)之間的函數關系式為:
(天)之間的函數關系式為: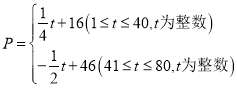 ,日銷售量
,日銷售量![]() (千克)與時間第
(千克)與時間第![]() (天)之間的函數關系如圖所示:
(天)之間的函數關系如圖所示:
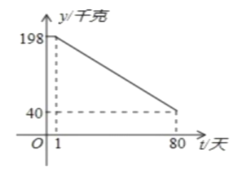
(1)求日銷售量![]() 與時間
與時間![]() 的函數關系式?
的函數關系式?
(2)哪一天的日銷售利潤最大?最大利潤是多少?
(3)在實際銷售的前![]() 天中,該養殖戶決定銷售
天中,該養殖戶決定銷售![]() 千克小龍蝦,就捐贈
千克小龍蝦,就捐贈![]() 元給村里的特困戶,在這前
元給村里的特困戶,在這前![]() 天中,每天扣除捐贈后的日銷售利潤隨時間
天中,每天扣除捐贈后的日銷售利潤隨時間![]() 的增大而增大,求
的增大而增大,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校八年級共400名學生,為了解該年級學生的視力情況,從中隨機抽取40名學生的視力數據作為樣本,數據統計如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根據數據繪制了如下的表格和統計圖:
等級 | 視力(x) | 頻數 | 頻率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合計 | 40 | 1 | |
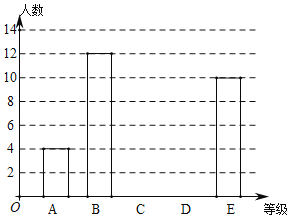
根據上面提供的信息,回答下列問題:
(1)統計表中的![]() ,
,![]() ;
;
(2)請補全條形統計圖;
(3)根據抽樣調查結果,請估計該校八年級學生視力為“![]() 級”的有多少人?
級”的有多少人?
(4)該年級學生會宣傳部有2名男生和2名女生,現從中隨機挑選2名同學參加“防控近視,愛眼護眼”宣傳活動,請用樹狀圖法或列表法求出恰好選中“1男1女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知銳角∠AOB如圖,(1)在射線OA上取一點C,以點O為圓心,OC長為半徑作![]() ,交射線OB于點D,連接CD;
,交射線OB于點D,連接CD;
(2)分別以點C,D為圓心,CD長為半徑作弧,交![]() 于點M,N;
于點M,N;
(3)連接OM,MN.
根據以上作圖過程及所作圖形,下列結論中錯誤的是( )

A. ∠COM=∠CODB. 若OM=MN,則∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC和△DEF均為等腰直角三角形,AB=2,DE=1,E、B、F、C在同一條直線上,開始時點B與點F重合,讓△DEF沿直線BC向右移動,最后點C與點E重合,設兩三角形重合面積為y,點F移動的距離為x,則y關于x的大致圖象是( )

A.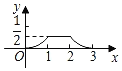 B.
B.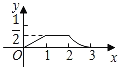
C.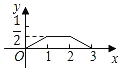 D.
D.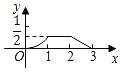
查看答案和解析>>
科目:初中數學 來源: 題型:
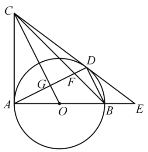
【題目】如圖,已知AB為⊙O的直徑,AC為⊙O的切線,連結CO,過B作BD∥OC交⊙O于D,連結AD交OC于G.延長AB、CD交于點E.
(1)求證:CD是⊙O的切線;
(2)若BE=2,DE=4,求CD的長;
(3)在(2)的條件下,連結BC交AD于F,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
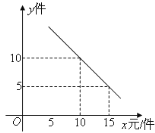
【題目】某文具零售店準備從批發市場選購A、B兩種文具,批發價A種為12元/件,B種為8元/件.若該店零售A、B兩種文具的日銷售量y(件)與零售價x(元/件)均成一次函數關系.(如圖)
(1)求y與x的函數關系式;
(2)該店計劃這次選購A、B兩種文具的數量共120件,所花資金不超過1200元,并希望全部售完獲利不低于178元,若按A種文具日銷售量6件和B種文具每件可獲利1元計算,則該店這次有哪幾種進貨方案?
(3)若A種文具的零售價比B種文具的零售價高4元/件,求兩種文具每天的銷售利潤(元)與A種文具零售價x(元/件)之間的函數關系式,并說明A、B兩種文具零售價分別為多少時,每天銷售的利潤最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com