
2009年云南省曲靖一中高考沖刺卷文科數學 (四)
(四)
本試卷分第Ⅰ卷(選擇題)和第Ⅱ卷(非選擇題)兩部分,滿分150分,考試時間120分鐘.
第Ⅰ卷(選擇題,共60分)
一、選擇題:本大題共12小題,每小題5分,共60分.在每小題給出的四個選項中,只
有一項是符合題目要求的.
1.設全集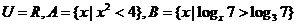 ,則
,則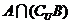 是
是
A.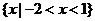 B.
B.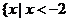 或
或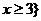

C.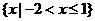 D.
D.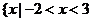 且
且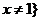

2.若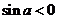 ,且
,且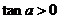 ,則
,則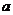 是
是
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
3.已知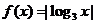 ,則下列不等式成立的是
,則下列不等式成立的是
A.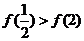 B.
B.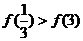 C.
C.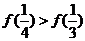 D.
D.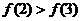

4.設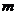 、
、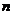 是不同的直線,
是不同的直線,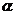 、
、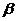 、
、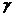 是不同的平面,有以下四個命題:
是不同的平面,有以下四個命題:
① 若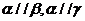 ,則
,則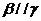 ② 若
② 若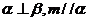 ,則
,則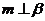

③ 若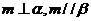 ,則
,則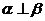 ④ 若
④ 若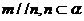 ,則
,則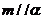

其中真命題的序號是
A.①④ B.②③ C.②④ D.①③
5.“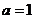 ”是“直線
”是“直線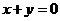 和直線
和直線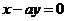 互相垂直”的
互相垂直”的
A.充分而不必要條件 B.必要而不充分條件
C.充要條件 D.既不充分也不必要條件
6.設等差數列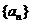 的前
的前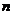 項和為
項和為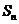 ,若
,若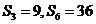 ,則
,則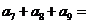

A.63 B.


7.從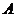 、
、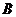 、
、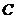 、
、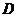 、
、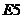 名短跑運動員中任選4名,排在標號分別為1、2、3、4的跑
名短跑運動員中任選4名,排在標號分別為1、2、3、4的跑
道上,則不同的排法有
A.24種 B.48種 C.120種 D.124種
8.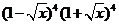 的展開式中
的展開式中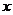 的系數是
的系數是
A.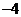 B.
B. C.3 D.4
C.3 D.4
9.設雙曲線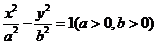 的離心率為
的離心率為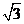 ,且它的一條準線為
,且它的一條準線為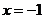 ,
,
則此雙曲線的方程為
A.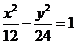 B.
B.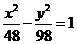 C.
C.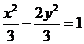 D.
D.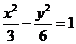

10.已知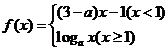 是
是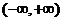 上的增函數,那么
上的增函數,那么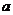 的取值范圍是
的取值范圍是
A.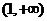 B.
B.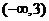 C.
C.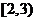 D.(1,3)
D.(1,3)
11.設 為曲線
為曲線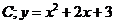 上的點,且曲線
上的點,且曲線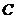 在點
在點 處切線傾斜角的取值范圍為
處切線傾斜角的取值范圍為
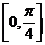 ,則點
,則點 縱坐標的取值范圍為
縱坐標的取值范圍為
A.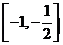 B.
B.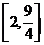 C.
C.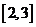 D.
D.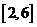

12.已知函數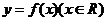 滿足
滿足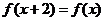 ,且當
,且當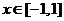 時,
時,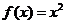 ,則
,則
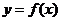 與
與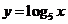 的圖象的交點個數為
的圖象的交點個數為
A.3 B.4 C.5 D.6

第Ⅱ卷(非選擇題,共90分)
二、填空題:本大題共4小題。每小題5分.共16分.把答案填在題中橫線上.
13.已知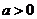 ,若平面上的三點
,若平面上的三點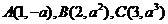 共線,則
共線,則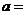 .
.
14.在正方體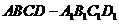 中,
中,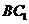 與平面
與平面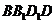 所成的角為
.
所成的角為
.
15.已知實數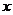 、
、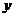 滿足條件
滿足條件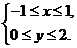 則函數
則函數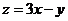 的最大值是
.
的最大值是
.
16.給出下列3個命題:
① 命題“存在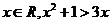 ”的否定是“任意
”的否定是“任意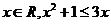 ”;
”;
② “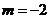 ”是“直線
”是“直線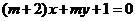 與直線
與直線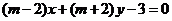 相互垂直”的必要不充分條件;
相互垂直”的必要不充分條件;
③ 關于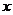 的不等式
的不等式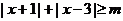 的解集為
的解集為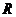 ,則
,則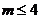 .
.
其中為真命題的序號是
.
三、解答題:本大題共6小題,共74分,解答應寫出文宇說明、證明過程或演算步驟.
17.(本小題滿分12分)
已知函數 的最小正周期為
的最小正周期為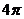 .
.
(1)求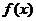 的單調遞增區間;
的單調遞增區間;
(2)在 中,角
中,角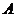 ,
,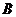 ,
,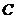 的對邊長分別是
的對邊長分別是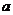 ,
,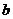 ,
,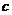 滿足
滿足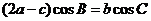 ,求函數
,求函數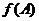 的取值范圍.
的取值范圍.


18.(本小題滿分12分)
在舉辦的奧運知識有獎問答競賽中,甲、乙、丙同時回答一道有關奧運知識的問題,已知甲答對這道題目的概率是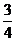 ,甲、丙兩人都答錯的概率是
,甲、丙兩人都答錯的概率是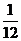 ,乙、丙兩人都答對的概率是
,乙、丙兩人都答對的概率是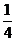 .
.
(1)求乙、丙兩人各自答對這道題目的概率;
(2)求甲、乙、丙三人中至少有兩人答對這道題目的概率.





19.(本小題滿分12分)
已知二次函數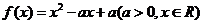 ,不等式
,不等式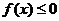 的解集有且只有一個元素,設數列
的解集有且只有一個元素,設數列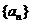 的前
的前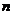 項和
項和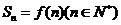

(1)求數列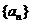 的通項公式;
的通項公式;
(2)設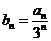 ,求數列
,求數列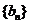 的前
的前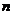 項和
項和 .
.

20.(本小題滿分12分)
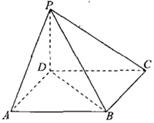 已知四棱錐
已知四棱錐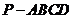 的底面
的底面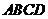 是正方形,且
是正方形,且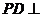 底面
底面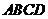 ,其中
,其中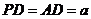 .
.
(1)求二面角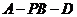 的大小;
的大小;
(2)在線段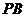 上是否存在一點
上是否存在一點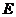 ,使
,使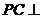 平面
平面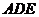 ?若存在,試確定
?若存在,試確定 點的位置;若不存在,請說明理由.
點的位置;若不存在,請說明理由.


21.(本小題滿分12分)
已知圓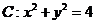 .
.
(1)直線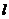 過點
過點 (1,2),且與圓
(1,2),且與圓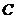 交于
交于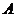 、
、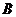 兩點,若
兩點,若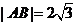 ,求直線
,求直線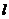 的方程;
的方程;
(2)過圓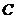 上一動點
上一動點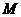 作平行于
作平行于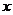 軸的直線
軸的直線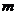 ,設
,設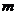 與
與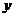 軸的交點為
軸的交點為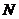 ,若向量
,若向量 ,求動點
,求動點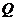 的軌跡方程,并說明此軌跡是什么曲線.
的軌跡方程,并說明此軌跡是什么曲線.

22.(本小題滿分12分)
設函數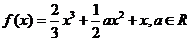 .
.
(1)當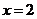 時,
時,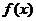 取得極值,求
取得極值,求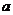 的值;
的值;
(2)若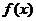 在
在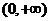 內為增函數,求
內為增函數,求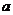 的取值范圍.
的取值范圍.

一、
1.C 2.C 3.C 4.D 5.C 6.B 7.C 8.A 9.D 10.C 
11.B 12.B
【解析】
11.提示:設曲線 在點
在點 處切線傾斜角為
處切線傾斜角為 ,則
,則 ,由
,由 ,得
,得 ,故
,故 ,所以
,所以 ,故選B.
,故選B.
12.提示:整形結合.
二、
13. 14.
14. 15.3 16.①③
15.3 16.①③
三、
17.解:(1)


 的單調遞增區間為
的單調遞增區間為
(2)




18.(1)設乙、丙各自回答對的概率分別是 、
、 ,根據題意得:
,根據題意得:
 ,解得
,解得
(2) .
.
19.解:(1) 的解集有且只有一個元素
的解集有且只有一個元素
 或
或
又由 得
得
當 時,
時, ;
;
當 時,
時,

(2) ①
①
 ②
②
由式①-或②得
 .
.
20.解法一:

(1)設 交
交 于點
于點
 平面
平面 .
.
作 于點
于點 ,連接
,連接 ,則由三垂線定理知:
,則由三垂線定理知: 是二面角
是二面角 的平面角.
的平面角.
由已知得 ,
,
 ,
,
∴二面角 的大小的60°.
的大小的60°.
(2)當 是
是 中點時,有
中點時,有 平面
平面 .
.
證明:取 的中點
的中點 ,連接
,連接 、
、 ,則
,則 ,
,
 ,故平面
,故平面 即平面
即平面 .
.
 又
又 平面
平面 ,
,
 平面
平面 .
.
解法二:由已知條件,以 為原點,以
為原點,以 、
、 、
、 為
為 軸、
軸、 軸、
軸、 軸建立空間直角坐標系,則
軸建立空間直角坐標系,則

(1) ,
,
 ,設平面
,設平面 的一個法向量為
的一個法向量為 ,
,
則 取
取
設平面 的一個法向量為
的一個法向量為 ,則
,則 取
取 .
.
 二面角
二面角 的大小為60°.
的大小為60°.
(2)令 ,則
,則 ,
,
 ,
,
由已知, ,要使
,要使 平面
平面 ,只需
,只需 ,即
,即
則有 ,得
,得 當
當 是
是 中點時,有
中點時,有 平面
平面 .
.
21.解:(1)① 當直線 垂直于
垂直于 軸時,則此時直線方程為
軸時,則此時直線方程為 ,
,
 與圓的兩個交點坐標為
與圓的兩個交點坐標為 和
和 ,其距離為
,其距離為 ,滿足題意.
,滿足題意.
② 若直線 不垂直于
不垂直于 軸,設其方程
軸,設其方程 ,即
,即
設圓心到此直線的距離為 ,則
,則 ,得
,得
 ,
,
此時所求直線方程為
綜上所述,所求直線為 或
或 .
.
(2)設點 的坐標為
的坐標為 點坐標為
點坐標為 ,則
,則 點坐標是
點坐標是

即
又 由已知,直線
由已知,直線 軸,所以,
軸,所以, ,
,
 點的軌跡議程是
點的軌跡議程是 ,
,
軌跡是焦點坐標為 ,長軸為8的橢圓,并去掉
,長軸為8的橢圓,并去掉 兩點.
兩點.
22.解: ,
,
(1)由題意: 解得
解得 .
.
(2)方程 的叛別式
的叛別式 ,
,
① 當 ,即
,即 時,
時, ,
, 在
在 內恒成立,此時
內恒成立,此時 在
在 為增函數;
為增函數;
② 當 ,即
,即 或
或 時,
時,
要使 在
在 內為增函數,只需在
內為增函數,只需在 內有
內有 即可,
即可,
設 ,
,
由 得
得 ,所以
,所以 .
.
由①②可知,若 在
在 內為增函數,則
內為增函數,則 的取值范圍是
的取值范圍是 .
.
www.ks5u.com
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com