
洛陽一高2008―2009學年下期高三年級2月月考
數 學 試 卷(理科)

本試卷分第I卷(選擇題)和第II卷(非選擇題)兩部分,滿分150分。

第I卷(選擇題 共60分)
注意事項:
1、答第I卷前,考生務必將自己的姓名、準考證號、考試科目用鉛筆涂寫在答題卡上。
2、每小題選出答案后,用鉛筆把答題卡上對應題目的答案標號涂黑。如需改動,用橡皮擦干凈后,再選涂其它答案,不能答在試題卷上。
3、考試結束,將第II卷和答題卡一并交回。
一、選擇題(每題5分)
1、已知集合M=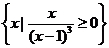 ,N=
,N= 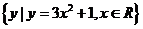 ,則
,則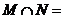

A、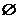 B、
B、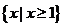 C、
C、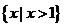 D、
D、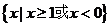

2、若p、q為簡單命題,則“p且q為假”是“p或q為假”的
A、充分不必要條件 B、必要不充分條件 C、充要條件 D、既不充分也不必要條件
3、向量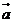 和
和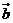 的夾角平分線上的單位向量是
的夾角平分線上的單位向量是
A、向量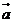 和
和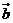 B、
B、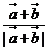 C、
C、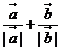 D、
D、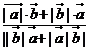

4、y=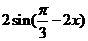 的單調增函區間是
的單調增函區間是
A、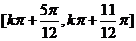 B、
B、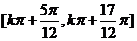

C、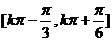 D、
D、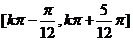 以上
以上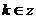

5、若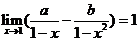 ,則常數a、b的值為
,則常數a、b的值為
A、 2 , 4 B、2,
2 , 4 B、2,
 2,
2,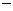 4 D、2,4
4 D、2,4
6、已知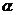 、
、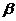 是兩個不同的平面,m、n是兩條不同的直線,給出下列命題
是兩個不同的平面,m、n是兩條不同的直線,給出下列命題
①若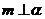 ,
,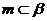 則
則 ②
②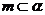 ,
, 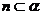
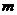 ∥
∥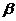 ,n∥
,n∥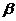 則
則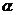 ∥
∥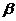

③如果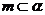 ,
,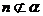 ,
,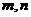 是異面直線,那么n與
是異面直線,那么n與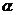 相交
相交
④若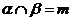 ,n∥m 且
,n∥m 且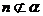 ,
,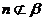 則n∥
則n∥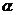 且n∥
且n∥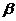

其中正確的命題:
A、①②
B、②③
C、③④
D、①④
7、若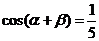
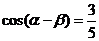 則
則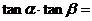

A、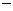 2 B、
2 B、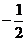 C、2
D、
C、2
D、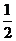

8、設偶函數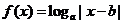 在(
在(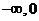 )上遞增,則
)上遞增,則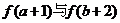 的大小關系是
的大小關系是
A、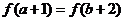 B、
B、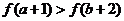 C、
C、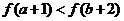 D、不確定
D、不確定
9、已知等比數列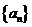 中,
中,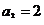 ,則其前3項的和
,則其前3項的和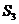 的取值范圍是
的取值范圍是
A、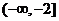 B、
B、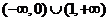 C、
C、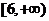 D、
D、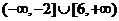

10、設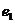 、
、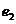 分別為具有公共焦點
分別為具有公共焦點 、
、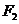 的橢圓和雙曲線的離心率,P為兩曲線的一個公共點,且滿足
的橢圓和雙曲線的離心率,P為兩曲線的一個公共點,且滿足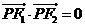 ,則
,則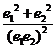 的值為
的值為
A、 1
B、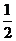 C、2
D、不確定
C、2
D、不確定
11、已知定義在R上的函數f(x),g(x) 滿足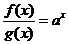 且
且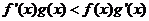
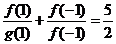 ,則有窮數列
,則有窮數列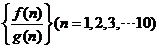 的前n項和大于
的前n項和大于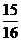 的概率是
的概率是
A、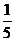 B、
B、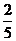 C、
C、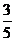 D、
D、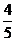

12、為提高信息在傳輸中的抗干擾能力,通常在原信息中按一定規則加入相關數據組成傳輸信息,設原信息為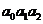 ,
,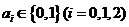 ,傳輸信息為
,傳輸信息為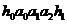 其中
其中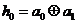
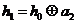
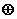 運算規則為0
運算規則為0 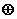 0=0,0
0=0,0 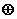 1=1,1
1=1,1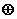 0=1,1
0=1,1 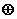 1=0;例如原信息為111,則傳輸信息為01111,轉輸信息在傳輸過程中受到干擾可能導致接收信息出錯,則下列接收信息一定有誤的是
1=0;例如原信息為111,則傳輸信息為01111,轉輸信息在傳輸過程中受到干擾可能導致接收信息出錯,則下列接收信息一定有誤的是
A、11010 B、




洛陽一高2008―2009學年下期高三年級2月月考
數 學 試 卷(理科)
第II卷(共90分)
注意事項:
1、第II卷共4頁,用鋼筆或圓珠筆直接寫在試題卷上。
2、答卷前將密封線內的項目填寫清楚。
題 號
一
二
三
總 分
1―12
13―16
17
18
19
20
21
22
得 分
二、填空題(每題5分)
13、設曲線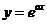 在點(0,1)處的切線與
在點(0,1)處的切線與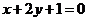 垂直則a=___________
垂直則a=___________
14、在“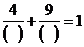 ”中的“( )”處分別填上一個自然數,并使它們的和最小
”中的“( )”處分別填上一個自然數,并使它們的和最小
15、在正方體的8個頂點中任意選擇4個頂點,它們可能是如下幾何圖形的4個頂點,這些幾何圖形是__________(寫出所有正確結論的編號)
①梯形
②矩形

③有三個面為等腰直角三角形,有一個面為等邊三角形的四面體
④每個面都是等邊三角形的四面體
⑤每個面都是等腰直角三角形的四面體
16、已知動點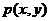 在橢圓
在橢圓 ,若點A坐標為(3,0)
,若點A坐標為(3,0) ,且
,且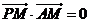 ,則
,則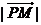 的最小值為_______________。
的最小值為_______________。
三、解答題:
17、(10分)在△ABC中,角A、B、C的對邊分別為a、b、c且滿足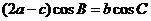

(1)求角B的大小
(2)設
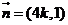 ,(k>1)且
,(k>1)且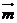 、
、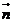 的最大值為5,求k的值。
的最大值為5,求k的值。








18、(12分)已知函數f(x)的圖像與函數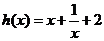 的圖像關于點A(0,1)對稱
的圖像關于點A(0,1)對稱
(1)求f (x)的解析式。
(2)若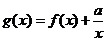 且
且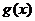 在區間(0,2]上為減函數,求實數a的取值范圍
在區間(0,2]上為減函數,求實數a的取值范圍










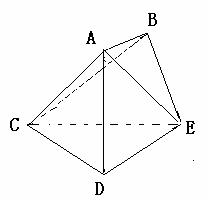 19、(12分)已知多面體ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1
19、(12分)已知多面體ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1
(1)求直線AE與平面CDE所成角的大小
(用反三角函數值表示)
(2)求多面體ABCDE的體積







20、(12分)已知函數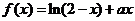

(1)設曲線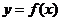 在點(1,f (1))處的切線為l ,若l 與圓
在點(1,f (1))處的切線為l ,若l 與圓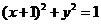 相切,求a的值
相切,求a的值
(2)當a>0時,求函數f (x)的單調區間


21、(12分)觀察下列三角形數表