
科目: 來源: 題型:
【題目】足球是當今世界傳播范圍最廣、參與人數最多的體育運動,具有廣泛的社會影響,深受世界各國民眾喜愛.
(1)為調查大學生喜歡足球是否與性別有關,隨機選取50名大學生進行問卷調查,當問卷評分不低于80分則認為喜歡足球,當評分低于80分則認為不喜歡足球,這50名大學生問卷評分的結果用莖葉圖表示如圖:
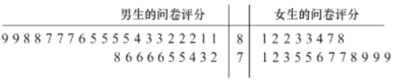
請依據上述數據填寫如下列聯表:
喜歡足球 | 不喜歡足球 | 總計 | |
女生 |
|
|
|
男生 |
|
|
|
總計 |
|
|
|
請問是否有 ![]() 的把握認為喜歡足球與性別有關?
的把握認為喜歡足球與性別有關?
參考公式及數據: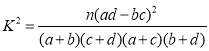 ,
,![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
(2)已知某國“糖果盒”足球場每年平均上座率![]() 與該國成年男子國家足球隊在國際足聯的年度排名
與該國成年男子國家足球隊在國際足聯的年度排名![]() 線性相關,數據如表
線性相關,數據如表![]() ,
,![]() ,
,![]() ,
,![]()
年度排名 | 9 |
| 6 |
| 3 |
平均上座率 | 0.9 | 0.91 | 0.92 | 0.93 | 0.95 |
求變量![]() 與
與![]() 的線性回歸方程
的線性回歸方程![]() ,并預測排名為1時該球場的上座率.
,并預測排名為1時該球場的上座率.
參考公式及數據: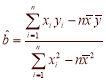 ,
,![]() ;
;![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】在平面直角坐標系中,動點![]() 分別與兩個定點
分別與兩個定點![]() ,
,![]() 的連線的斜率之積為
的連線的斜率之積為![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設過點![]() 的直線與軌跡
的直線與軌跡![]() 交于
交于![]() ,
,![]() 兩點,判斷直線
兩點,判斷直線![]() 與以線段
與以線段![]() 為直徑的圓的位置關系,并說明理由.
為直徑的圓的位置關系,并說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】《九章算術》是我國古代數學文化的優秀遺產,數學家劉徽在注解《九章算術》時,發現當圓內接正多邊行的邊數無限增加時,多邊形的面積可無限逼近圓的面積,為此他創立了割圓術,利用割圓術,劉徽得到了圓周率精確到小數點后四位3.1416,后人稱3.14為徽率,如圖是利用劉徽的割圓術設計的程序框圖,若結束程序時,則輸出的![]() 為( )(
為( )(![]() ,
,![]() ,
,![]() )
)

A. 6 B. 12 C. 24 D. 48
查看答案和解析>>
科目: 來源: 題型:
【題目】某家庭記錄了未使用節水龍頭50天的日用水量數據(單位:m3)和使用了節水龍頭50天的日用水量數據,得到頻數分布表如下:
未使用節水龍頭50天的日用水量頻數分布表
日用 水量 |
|
|
|
|
|
|
|
頻數 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了節水龍頭50天的日用水量頻數分布表
日用 水量 |
|
|
|
|
|
|
頻數 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答題卡上作出使用了節水龍頭50天的日用水量數據的頻率分布直方圖:
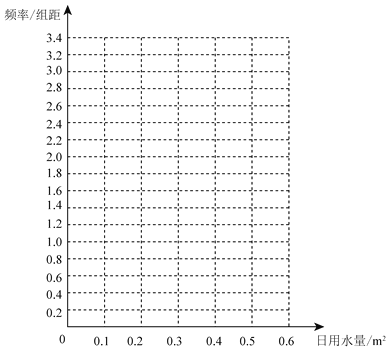
(2)估計該家庭使用節水龍頭后,日用水量小于0.35 m3的概率;
(3)估計該家庭使用節水龍頭后,一年能節省多少水?(一年按365天計算,同一組中的數據以這組數據所在區間中點的值作代表.)
查看答案和解析>>
科目: 來源: 題型:
【題目】在極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,以極點為原點
,以極點為原點![]() ,極軸為
,極軸為![]() 軸正半軸(兩坐標系取相同的單位長度)的直角坐標系
軸正半軸(兩坐標系取相同的單位長度)的直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為:
的參數方程為:![]() 為參數).
為參數).
(1)求曲線![]() 的直角坐標方程與曲線
的直角坐標方程與曲線![]() 的普通方程;
的普通方程;
(2)將曲線![]() 經過伸縮變換
經過伸縮變換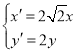 后得到曲線
后得到曲線![]() ,若
,若![]() ,
,![]() 分別是曲線
分別是曲線![]() 和曲線
和曲線![]() 上的動點,求
上的動點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 來源: 題型:
【題目】某省高考改革實施方案指出:該省高考考生總成績將由語文、數學、外語3門統一高考成績和學生自主選擇的學業水平等級性考試科目共同構成.該省教育廳為了解正就讀高中的學生家長對高考改革方案所持的贊成態度,隨機從中抽取了100名城鄉家長作為樣本進行調查,調查結果顯示樣本中有25人持不贊成意見.如圖是根據樣本的調查結果繪制的等高條形圖.
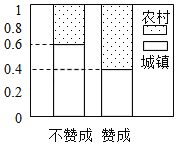
(1)根據已知條件與等高條形圖完成下面的2×2列聯表,并判斷我們能否有95%的把握認為“贊成高考改革方案與城鄉戶口有關”?
贊成 | 不贊成 | 合計 | |
城鎮居民 | |||
農村居民 | |||
合計 |
(2)利用分層抽樣從持“不贊成”意見家長中抽取5名參加學校交流活動,從中選派2名家長發言,求恰好有1名城鎮居民的概率.
附: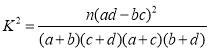 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com