
【題目】已知函數![]() .
.
(1)若函數![]() 在x=2處取得極值,求
在x=2處取得極值,求![]() 的極大值;
的極大值;
(2)若![]() 對
對![]() 成立,求實數a的取值范圍.
成立,求實數a的取值范圍.
【答案】(1)極大值為![]() ;(2)
;(2)![]()
【解析】試題分析:(1)求導,根據條件得![]() ,進而檢驗即可;
,進而檢驗即可;
(2)據題意,得![]() 對
對![]() 恒成立,令
恒成立,令![]() ,
,![]() ,分情況
,分情況![]() ,
,![]() ,
,![]() 和
和![]() 時,求最小值即可.
時,求最小值即可.
試題解析:
(1)∵![]() ,∴
,∴![]() .
.
又∵函數![]() 在
在![]() 處取得極值,
處取得極值,
∴![]() ,解得
,解得![]() .
.
當![]() 時,
時,![]() .
.
令![]() ,則
,則![]() ,∴
,∴![]() ,
,![]() .
.
|
| 1 |
| 2 |
|
| + | 0 | - | 0 | + |
| 單調遞增 | 極大值 | 單調遞減 | 極小值 | 單調遞增 |
![]() 的極大值為
的極大值為![]() .
.
(2)據題意,得![]() 對
對![]() 恒成立.
恒成立.
設![]() ,則
,則![]() .
.
討論:
(i)當![]() 時,由
時,由![]() 得函數
得函數![]() 單調減區間為
單調減區間為![]() ;由
;由![]() 得函數
得函數![]() 單調增區間為
單調增區間為![]() .
.
∴![]() ,且
,且![]() .
.
∴![]() ,解得
,解得![]() ;
;
(ii)當![]() 時,由
時,由![]() 得函數
得函數![]() 單調減區間
單調減區間![]() ;由
;由![]() 得函數
得函數![]() 單調增區間為
單調增區間為![]() ,
,![]() ,
,
又![]() ,不合題意.
,不合題意.
(iii)當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增,
上單調遞增,
又![]() ,不合題意.
,不合題意.
(iv)當![]() 時,由
時,由![]() 得函數
得函數![]() 單調減區間為
單調減區間為![]() ;由
;由![]() 得函數
得函數![]() 單調增區間
單調增區間![]() ,
,![]() ,又
,又![]() ,不合題意.
,不合題意.
綜上,所求實數a的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】已知二次函數![]() .
.
(1)已知![]() 的解集為
的解集為![]() ,求實數
,求實數![]() 的值;
的值;
(2)已知![]() ,設
,設![]() 、
、![]() 是關于
是關于![]() 的方程
的方程![]() 的兩根,且
的兩根,且![]() ,求實數
,求實數![]() 的值;
的值;
(3)已知![]() 滿足
滿足![]() ,且關于
,且關于![]() 的方程
的方程![]() 的兩實數根分別在區間
的兩實數根分別在區間![]() 內,求實數
內,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,AB=2AD,
中,AB=2AD,![]() 為DC的中點,將△ADM沿AM折起使平面ADM⊥平面ABCM.
為DC的中點,將△ADM沿AM折起使平面ADM⊥平面ABCM.
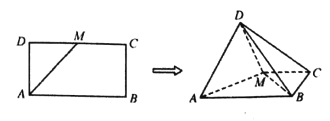
(1)當AB=2時,求三棱錐![]() 的體積;
的體積;
(2)求證:BM⊥AD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市周年慶典,設置了一項互動游戲如圖,一個圓形游戲轉盤被分成6個均勻的扇形區域.用力旋轉轉盤,轉盤停止轉動時,箭頭![]() 所指區域的數字就是每次游戲所得的分數(箭頭指向兩個區域的邊界時重新轉動),且箭頭
所指區域的數字就是每次游戲所得的分數(箭頭指向兩個區域的邊界時重新轉動),且箭頭![]() 指向每個區域的可能性都是相等的.要求每個家庭派一名兒童和一位成人先后各轉動一次游戲轉盤,記為
指向每個區域的可能性都是相等的.要求每個家庭派一名兒童和一位成人先后各轉動一次游戲轉盤,記為![]() ,若一個家庭總得分
,若一個家庭總得分![]() ,假設兒童和成人的得分互不影響,且每個家庭只能參加一次活動,游戲規定:
,假設兒童和成人的得分互不影響,且每個家庭只能參加一次活動,游戲規定:

①若![]() ,則該家庭可以獲得一等獎一份;
,則該家庭可以獲得一等獎一份;
②若![]() ,則該家庭可以獲得二等獎一份;
,則該家庭可以獲得二等獎一份;
若![]() ,則該家庭可以獲得紀念獎一份.
,則該家庭可以獲得紀念獎一份.
(1)求一個家庭獲得紀念獎的概率;
(2)試比較同一個家庭獲得一等獎和二等獎概率的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中![]() 中,直線
中,直線![]() ,圓
,圓![]() 的參數方程為
的參數方程為![]() 為參數),以坐標原點為極點,以
為參數),以坐標原點為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求直線![]() 和圓
和圓![]() 的極坐標方程;
的極坐標方程;
(2)若直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,且
兩點,且![]() 的面積是
的面積是![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
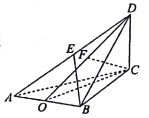
【題目】[2018·郴州期末]已知三棱錐![]() 中,
中,![]() 垂直平分
垂直平分![]() ,垂足為
,垂足為![]() ,
,![]() 是面積為
是面積為![]() 的等邊三角形,
的等邊三角形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,垂足為
,垂足為![]() ,
,![]() 為線段
為線段![]() 的中點.
的中點.
(1)證明:![]() 平面
平面![]() ;
;
(2)求![]() 與平面
與平面![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設全集U=R,集合![]() ,B={y|y=2x,x≤1},C={x|2a<x<a+1}.
,B={y|y=2x,x≤1},C={x|2a<x<a+1}.
(1)求A∩UB;
(2)若C(A∪B),求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com