
【題目】已知函數(shù)![]() ,
,![]() ,
,![]() .
.
(1)當(dāng)![]() ,
,![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的最小值;
的最小值;
(2)當(dāng)![]() ,
,![]() 時(shí),求證方程
時(shí),求證方程![]() 在區(qū)間
在區(qū)間![]() 上有唯一實(shí)數(shù)根;
上有唯一實(shí)數(shù)根;
(3)當(dāng)![]() 時(shí),設(shè)
時(shí),設(shè)![]() 是
是![]() 函數(shù)兩個(gè)不同的極值點(diǎn),證明:
函數(shù)兩個(gè)不同的極值點(diǎn),證明:![]() .
.
【答案】(1)![]() (2)見(jiàn)解析(3)見(jiàn)解析
(2)見(jiàn)解析(3)見(jiàn)解析
【解析】
(1)構(gòu)造新函數(shù)y=![]() ,求導(dǎo)判斷單調(diào)性,得出最小值e.(2)變量分離a=-
,求導(dǎo)判斷單調(diào)性,得出最小值e.(2)變量分離a=-![]() =h(x),根據(jù)函數(shù)的單調(diào)性求出函數(shù)h(x)的最小值,利用a的范圍證明在區(qū)間(0,2)上有唯一實(shí)數(shù)根;(3)求出
=h(x),根據(jù)函數(shù)的單調(diào)性求出函數(shù)h(x)的最小值,利用a的范圍證明在區(qū)間(0,2)上有唯一實(shí)數(shù)根;(3)求出![]() ,問(wèn)題轉(zhuǎn)化為證
,問(wèn)題轉(zhuǎn)化為證![]() ,令x1﹣x2=t,得到t<0,根據(jù)函數(shù)的單調(diào)性證明即可.
,令x1﹣x2=t,得到t<0,根據(jù)函數(shù)的單調(diào)性證明即可.
(1)當(dāng)![]() =0,
=0,![]() 時(shí),
時(shí),![]() =
=![]() ,求導(dǎo)y’=
,求導(dǎo)y’=![]() =0的根x=1
=0的根x=1
所以y在(-![]() ),(0,1)遞減,在(1,+
),(0,1)遞減,在(1,+![]() )遞增,
)遞增,
所以y![]() =e
=e
(2)![]() +
+![]() =0,所以a=-
=0,所以a=-![]() =h(x)
=h(x)
H’(x)=-![]() =0的根x=2
=0的根x=2
則h(x)在(0,2)上單調(diào)遞增,在(2,+∞)上單調(diào)遞減,
所以h(2)是y=h(x)的極大值即最大值,即![]()
所以函數(shù)f(x)在區(qū)間(0,2)上有唯一實(shí)數(shù)根;
(3)![]() =
= ![]() -
-![]()
F’(x)![]() -2ax-a=0的兩根是
-2ax-a=0的兩根是![]() ,
,![]()
∵x1,x2是函數(shù)F(x)的兩個(gè)不同極值點(diǎn)(不妨設(shè)x1<x2),
∴a>0(若a≤0時(shí),f'(x)>0,即F(x)是R上的增函數(shù),與已知矛盾),
且F'(x1)=0,F(xiàn)'(x2)=0.∴![]() ,
,![]() …
…
兩式相減得: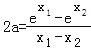 ,…
,…
于是要證明![]() ,即證明
,即證明 ,兩邊同除以
,兩邊同除以![]() ,
,
即證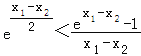 ,即證
,即證![]() ,即證
,即證![]() ,
,
令x1﹣x2=t,t<0.即證不等式![]() ,當(dāng)t<0時(shí)恒成立.
,當(dāng)t<0時(shí)恒成立.
設(shè)![]() ,∴
,∴![]() =
=![]()
設(shè)![]() ,∴
,∴![]() ,
,
當(dāng)t<0,h'(t)<0,h(t)單調(diào)遞減,
所以h(t)>h(0)=0,即![]() ,
,
∴φ'(t)<0,∴φ(t)在t<0時(shí)是減函數(shù).
∴φ(t)在t=0處取得極小值φ(0)=0.
∴φ(t)>0,得證.
∴![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 是定義域?yàn)?/span>R的奇函數(shù).
是定義域?yàn)?/span>R的奇函數(shù).
(1)求t的值;
(2)判斷![]() 在R上的單調(diào)性,并用定義證明;
在R上的單調(diào)性,并用定義證明;
(3)若函數(shù)![]() 在
在![]() 上的最小值為-2,求k的值.
上的最小值為-2,求k的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
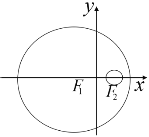
【題目】如圖,已知圓![]() 的方程為
的方程為![]() ,圓
,圓![]() 的方程為
的方程為![]() ,若動(dòng)圓
,若動(dòng)圓![]() 與圓
與圓![]() 內(nèi)切,與圓
內(nèi)切,與圓![]() 外切.
外切.
(Ⅰ)求動(dòng)圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過(guò)直線![]() 上的點(diǎn)
上的點(diǎn)![]() 作圓
作圓![]() 的兩條切線,設(shè)切點(diǎn)分別是
的兩條切線,設(shè)切點(diǎn)分別是![]() ,
,![]() ,若直線
,若直線![]() 與軌跡
與軌跡![]() 交于
交于![]() ,
,![]() 兩點(diǎn),求
兩點(diǎn),求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,離心率
,離心率![]() ,且橢圓的短軸長(zhǎng)為2.
,且橢圓的短軸長(zhǎng)為2.
(1)球橢圓的標(biāo)準(zhǔn)方程;
(2)已知直線![]() 過(guò)右焦點(diǎn)
過(guò)右焦點(diǎn)![]() ,且它們的斜率乘積為
,且它們的斜率乘積為![]() ,設(shè)
,設(shè)![]() 分別與橢圓交于點(diǎn)
分別與橢圓交于點(diǎn)![]() 和
和![]() .
.
①求![]() 的值;
的值;
②設(shè)![]() 的中點(diǎn)
的中點(diǎn)![]() ,
,![]() 的中點(diǎn)為,求
的中點(diǎn)為,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】給出下列命題,其中正確的序號(hào)是________(寫(xiě)出所有正確命題的序號(hào)).
①已知集合![]() ,
,![]() ,則映射
,則映射![]() 中滿足
中滿足![]() 的映射共有
的映射共有![]() 個(gè);
個(gè);
②函數(shù)![]() 的圖象關(guān)于
的圖象關(guān)于![]() 對(duì)稱的函數(shù)解析式為
對(duì)稱的函數(shù)解析式為![]() ;
;
③若函數(shù)![]() 的值域?yàn)?/span>
的值域?yàn)?/span>![]() ,則實(shí)數(shù)
,則實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]() ;
;
④已知函數(shù)![]() 的最大值為
的最大值為![]() ,最小值為
,最小值為![]() ,則
,則![]() 的值等于
的值等于![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】20名高二學(xué)生某次數(shù)學(xué)考試成績(jī)(單位:分)的頻率分布直方圖如圖:
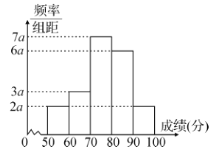
(1)求頻率分布直方圖中![]() 的值;
的值;
(2)分別求出成績(jī)落在![]() 與
與![]() 中的學(xué)生人數(shù);
中的學(xué)生人數(shù);
(3)從成績(jī)?cè)?/span>![]() 的學(xué)生中任選2人,求此2人的成績(jī)都在
的學(xué)生中任選2人,求此2人的成績(jī)都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=x2-2ax-1+a,a∈R.
(1)若a=2,試求函數(shù)y=![]() (x>0)的最小值;
(x>0)的最小值;
(2)對(duì)于任意的x∈[0,2],不等式f(x)≤a成立,試求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】隨著我國(guó)經(jīng)濟(jì)的發(fā)展,居民的儲(chǔ)蓄存款逐年增長(zhǎng)。設(shè)某地區(qū)城鄉(xiāng)居民人民幣儲(chǔ)蓄存款![]() (單位:億元)的數(shù)據(jù)如下:
(單位:億元)的數(shù)據(jù)如下:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代號(hào) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
儲(chǔ)蓄存款 | 3.4 | 3.6 | 4.5 | 4.9 | 5.5 | 6.1 | 7.0 |
(1)求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程;
的線性回歸方程;
(2)2018年城鄉(xiāng)居民儲(chǔ)蓄存款前五名中,有三男和兩女。現(xiàn)從這5人中隨機(jī)選出2人參加某訪談節(jié)目,求選中的2人性別不同的概率。
附:回歸直線的斜率和截距的最小二乘估計(jì)公式分別為: ,
,![]() 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() 、
、![]() ,圓
,圓![]() 經(jīng)過(guò)橢圓
經(jīng)過(guò)橢圓![]() 的兩個(gè)焦點(diǎn)和兩個(gè)頂點(diǎn),點(diǎn)
的兩個(gè)焦點(diǎn)和兩個(gè)頂點(diǎn),點(diǎn)![]() 在橢圓
在橢圓![]() 上,且
上,且![]() ,
,![]() .
.
(Ⅰ)求橢圓![]() 的方程和點(diǎn)
的方程和點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(Ⅱ)過(guò)點(diǎn)![]() 的直線
的直線![]() 與圓
與圓![]() 相交于
相交于![]() 、
、![]() 兩點(diǎn),過(guò)點(diǎn)
兩點(diǎn),過(guò)點(diǎn)![]() 與
與![]() 垂直的直線
垂直的直線![]() 與橢圓
與橢圓![]() 相交于另一點(diǎn)
相交于另一點(diǎn)![]() ,求
,求![]() 的面積的取值范圍.
的面積的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com