
【題目】如圖,已知圓![]() 的方程為
的方程為![]() ,圓
,圓![]() 的方程為
的方程為![]() ,若動圓
,若動圓![]() 與圓
與圓![]() 內切,與圓
內切,與圓![]() 外切.
外切.
(Ⅰ)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過直線![]() 上的點
上的點![]() 作圓
作圓![]() 的兩條切線,設切點分別是
的兩條切線,設切點分別是![]() ,
,![]() ,若直線
,若直線![]() 與軌跡
與軌跡![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的最小值.
的最小值.
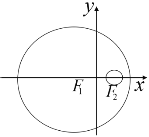
【答案】(1)![]() (2)
(2)![]()
【解析】
(Ⅰ)設動圓![]() 的半徑為
的半徑為![]() ,由題動圓
,由題動圓![]() 與圓
與圓![]() 內切,與圓
內切,與圓![]() 外切,則
外切,則
![]() ,由此即可得到動圓圓心
,由此即可得到動圓圓心![]() 的軌跡是以
的軌跡是以![]() 為焦點,長軸長為
為焦點,長軸長為![]() 的橢圓,進而得到動圓圓心
的橢圓,進而得到動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)設直線![]() 上任意一點
上任意一點![]() 的坐標是
的坐標是![]() ,切點
,切點![]() 坐標分別是
坐標分別是![]() ,
,
![]() ;則經過
;則經過![]() 點的切線斜方程是
點的切線斜方程是![]() ,同理經過
,同理經過![]() 點的切線方程是
點的切線方程是![]() ,又兩條切線
,又兩條切線![]() ,
,![]() 相交于
相交于![]()
![]() .可得經過
.可得經過![]() 兩點的直線
兩點的直線![]() 的方程是
的方程是![]() ,對
,對![]() 分類討論分別求出
分類討論分別求出![]() 的值,即可得到
的值,即可得到![]() 的最小值.
的最小值.
(Ⅰ)設動圓![]() 的半徑為
的半徑為![]() ,∵動圓
,∵動圓![]() 與圓
與圓![]() 內切,與圓
內切,與圓![]() 外切,
外切,
∴![]() ,且
,且![]() .于是,
.于是,![]() ,
,
所以動圓圓心![]() 的軌跡是以
的軌跡是以![]() 為焦點,長軸長為
為焦點,長軸長為![]() 的橢圓.從而,
的橢圓.從而,![]() ,
,
所以![]() .故動圓圓心
.故動圓圓心![]() 的軌跡
的軌跡![]() 的方程為
的方程為![]() .
.
(Ⅱ)設直線![]() 上任意一點
上任意一點![]() 的坐標是
的坐標是![]() ,切點
,切點![]() 坐標分別是
坐標分別是![]() ,
,
![]() ;則經過
;則經過![]() 點的切線斜率
點的切線斜率![]() ,方程是
,方程是![]() ,
,
經過![]() 點的切線方程是
點的切線方程是![]() ,又兩條切線
,又兩條切線![]() ,
,![]() 相交于
相交于![]()
![]() .
.
則有![]() ,所以經過
,所以經過![]() 兩點的直線
兩點的直線![]() 的方程是
的方程是![]() ,
,
①當![]() 時,有
時,有![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() ;
;
②當![]() 時,聯立
時,聯立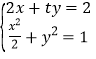 ,整理得
,整理得![]() ;
;
設![]() 坐標分別為
坐標分別為![]() ,
,![]() ,則
,則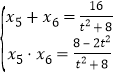 ,
,
所以![]() ,
,
綜上所述,當![]() 時,
時,![]() 有最小值
有最小值![]() .
.


科目:高中數學 來源: 題型:
【題目】為了解中學生課余觀看熱門綜藝節目“爸爸去哪兒”是否與性別有關,某中學一研究性學習小組從該校學生中隨機抽取了![]() 人進行問卷調查.調查結果表明:女生中喜歡觀看該節目的占女生總人數的
人進行問卷調查.調查結果表明:女生中喜歡觀看該節目的占女生總人數的![]() ,男生喜歡看該節目的占男生總人數的
,男生喜歡看該節目的占男生總人數的![]() .隨后,該小組采用分層抽樣的方法從這
.隨后,該小組采用分層抽樣的方法從這![]() 份問卷中繼續抽取了
份問卷中繼續抽取了![]() 份進行重點分析,知道其中喜歡看該節目的有
份進行重點分析,知道其中喜歡看該節目的有![]() 人.
人.
(1) 現從重點分析的![]() 人中隨機抽取了
人中隨機抽取了![]() 人進行現場調查,求這兩人都喜歡看該節目的概率;
人進行現場調查,求這兩人都喜歡看該節目的概率;
(2) 若有![]() 的把握認為“愛看該節目與性別有關”,則參與調查的總人數
的把握認為“愛看該節目與性別有關”,則參與調查的總人數![]() 至少為多少?
至少為多少?
參考數據:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面邊長為a,E是PC的中點.
(Ⅰ)求證:PA∥平面BDE;
(Ⅱ)平面PAC⊥平面BDE;
(Ⅲ)若二面角E-BD-C為30°,求四棱錐P-ABCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,
,![]() 是函數
是函數![]() 的圖像上任意不同的兩點,依據圖像可知,線段
的圖像上任意不同的兩點,依據圖像可知,線段![]() 總是位于
總是位于![]() 兩點之間函數圖像的上方,因此有結論
兩點之間函數圖像的上方,因此有結論![]() 成立,運用類比的思想方法可知,若點
成立,運用類比的思想方法可知,若點![]() ,
,![]() 是函數
是函數![]() 的圖像上任意不同的兩點,則類似地有_________成立.
的圖像上任意不同的兩點,則類似地有_________成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某投資公司對以下兩個項目進行前期市場調研:項目![]() :通信設備.根據調研,投資到該項目上,所有可能結果為:獲利
:通信設備.根據調研,投資到該項目上,所有可能結果為:獲利![]() 、損失
、損失![]() 、不賠不賺,且這三種情況發生的概率分別為
、不賠不賺,且這三種情況發生的概率分別為![]() ;項目
;項目![]() :新能源汽車.根據調研,投資到該項目上,所有可能結果為:獲利
:新能源汽車.根據調研,投資到該項目上,所有可能結果為:獲利![]() 、虧損
、虧損![]() ,且這兩種情況發生的概率分別為
,且這兩種情況發生的概率分別為![]() .經測算,當投入
.經測算,當投入![]() 兩個項目的資金相等時,它們所獲得的平均收益(即數學期望)也相等.
兩個項目的資金相等時,它們所獲得的平均收益(即數學期望)也相等.
(1)求![]() 的值;
的值;
(2)若將![]() 萬元全部投到其中的一個項目,請你從投資回報穩定性考慮,為投資公司選擇一個合理的項目,并說明理由.
萬元全部投到其中的一個項目,請你從投資回報穩定性考慮,為投資公司選擇一個合理的項目,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著“北京八分鐘”在韓國平昌冬奧會驚艷亮相,冬奧會正式進入了北京周期,全社會對冬奧會的熱情空前高漲.
(1)為迎接冬奧會,某社區積極推動冬奧會項目在社區青少年中的普及,并統計了近五年來本社區冬奧項目青少年愛好者的人數![]() (單位:人)與時間
(單位:人)與時間![]() (單位:年),列表如下:
(單位:年),列表如下:

依據表格給出的數據,是否可用線性回歸模型擬合![]() 與
與![]() 的關系,請計算相關系數
的關系,請計算相關系數![]() 并加以說明(計算結果精確到0.01).
并加以說明(計算結果精確到0.01).
(若![]() ,則線性相關程度很高,可用線性回歸模型擬合)
,則線性相關程度很高,可用線性回歸模型擬合)
附:相關系數公式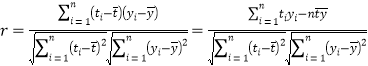 ,參考數據
,參考數據![]() .
.
(2)某冰雪運動用品專營店為吸引廣大冰雪愛好者,特推出兩種促銷方案.
方案一:每滿600元可減100元;
方案二:金額超過600元可抽獎三次,每次中獎的概率同為![]() ,且每次抽獎互不影響,中獎1次打9折,中獎2次打8折,中獎3次打7折. v
,且每次抽獎互不影響,中獎1次打9折,中獎2次打8折,中獎3次打7折. v
兩位顧客都購買了1050元的產品,并且都選擇第二種優惠方案,求至少有一名顧客比選擇方案一更優惠的概率;
②如果你打算購買1000元的冰雪運動用品,請從實際付款金額的數學期望的角度分析應該選擇哪種優惠方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com