
【題目】已知函數f(x)=x2-2ax-1+a,a∈R.
(1)若a=2,試求函數y=![]() (x>0)的最小值;
(x>0)的最小值;
(2)對于任意的x∈[0,2],不等式f(x)≤a成立,試求a的取值范圍.
科目:高中數學 來源: 題型:
【題目】已知f(x)=![]() ,x∈(-2,2).
,x∈(-2,2).
(1) 判斷f(x)的奇偶性并說明理由;
(2) 求證:函數f(x)在(-2,2)上是增函數;
(3) 若f(2+a)+f(1-2a)>0,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,定義:
,定義:![]() 表示不小于
表示不小于![]() 的最小整數,例如:
的最小整數,例如:![]() ,
,![]() .
.
(1)若![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(2)若![]() ,求
,求![]() 時實數
時實數![]() 的取值范圍;
的取值范圍;
(3)設![]() ,
,![]() ,若對于任意的
,若對于任意的![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年是中國改革開放40周年,改革開放40年來,從開啟新時期到跨入新世紀,從站上新起點到進人新時代,我們黨引領人民繪就了一幅波瀾壯闊、氣勢恢宏的歷史畫卷,譜寫了一曲感天動地、氣壯山河的奮斗贊歌,40年來我們始終堅持保護環境和節約資源,堅持推進生態文明建設,鄭州市政府也越來越重視生態系統的重建和維護,若市財政下撥一項專款100百萬元,分別用于植綠護綠和處理污染兩個生態維護項目,植綠護綠項目五年內帶來的生態收益可表示為投放資金x(單位:百萬元)的函數M(x(單位:百萬元):![]() ,處理污染項目五年內帶來的生態收益可表示為投放資金x(單位:百萬元)的函數N(x)(單位:百萬元):
,處理污染項目五年內帶來的生態收益可表示為投放資金x(單位:百萬元)的函數N(x)(單位:百萬元):![]() .
.
(Ⅰ)設分配給植綠護綠項目的資金為x(百萬元),則兩個生態項目五年內帶來的收益總和為y,寫出y關于x的函數解析式和定義域。
(Ⅱ)生態項目的投資開始利潤薄弱,只有持之以恒,才能功在當代,利在千秋,試求出y的最大值,并求出此時對兩個生態項目的投資分別為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xln x.
(1)求函數f(x)的極值點;
(2)設函數g(x)=f(x)-a(x-1),其中a∈R,求函數g(x)在區間[1,e]上的最小值.(其中e為自然對數的底數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我們把定義域為![]() 且同時滿足以下兩個條件的函數
且同時滿足以下兩個條件的函數![]() 稱為“
稱為“![]() 函數”:(1)對任意的
函數”:(1)對任意的![]() ,總有
,總有![]() ;(2)若
;(2)若![]() ,
,![]() ,則有
,則有![]() 成立,下列判斷正確的是( )
成立,下列判斷正確的是( )
A.若![]() 為“
為“![]() 函數”,則
函數”,則![]()
B.若![]() 為“
為“![]() 函數”,則
函數”,則![]() 在
在![]() 上為增函數
上為增函數
C.函數![]() 在
在![]() 上是“
上是“![]() 函數”
函數”
D.函數![]() 在
在![]() 上是“
上是“![]() 函數”
函數”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,多面體ABCDE中,四邊形ABED是直角梯形,∠BAD=90°,DE∥AB,△ACD是的正三角形,CD=AB=![]() DE=1,BC=
DE=1,BC=![]()
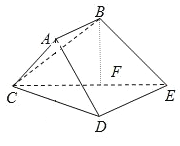
(1)求證:△CDE是直角三角形
(2) F是CE的中點,證明:BF⊥平面CDE
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com