
【題目】數(shù)列![]() ,
,![]() 滿足下列條件:①
滿足下列條件:①![]() ,
,![]() ;②當(dāng)
;②當(dāng)![]() 時,
時,![]() 滿足:
滿足:![]() 時,
時,![]() ,
,![]() ;
;![]() 時,
時,![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值,并猜想數(shù)列
的值,并猜想數(shù)列![]() 可能的通項公式(不需證明);
可能的通項公式(不需證明);
(2)若![]() ,
,![]() ,
,![]() 是滿足
是滿足![]() 的最大整數(shù),求
的最大整數(shù),求![]() 的值.
的值.
【答案】(1)見解析;(2)11.
【解析】
(1)利用題中的條件,分別令![]() ,求出
,求出![]() 和
和![]() 的值,并計算
的值,并計算![]() ,
,![]() ,
,![]() ,
,![]() ,根據(jù)這四項,猜想數(shù)列
,根據(jù)這四項,猜想數(shù)列![]() 可能的通項公式;
可能的通項公式;
(2)用反證法說明![]() 時,
時,![]() ,由此推出
,由此推出![]() ,從而得到
,從而得到![]() 通項公式,寫出
通項公式,寫出![]() 時
時![]() 通項公式,再由
通項公式,再由![]() 是滿足
是滿足![]() 的最大整數(shù),得到
的最大整數(shù),得到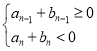 ,解之可得整數(shù)
,解之可得整數(shù)![]() .
.
(1)![]() ,
,![]() ,故
,故![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故![]() ,
,![]() ,
,![]() ,
,![]()
猜想:![]() .
.
(2)![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
當(dāng)![]() 時,假設(shè)存在
時,假設(shè)存在![]() 使得
使得![]() ,
,
則有![]() ,與“
,與“![]() 是滿足
是滿足![]() 的最大整數(shù)”矛盾,
的最大整數(shù)”矛盾,
![]() 假設(shè)不成立,
假設(shè)不成立,
![]()
![]() 時,恒有
時,恒有![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() 是以
是以![]() 為首項,
為首項,![]() 為公比的等比數(shù)列,
為公比的等比數(shù)列,
![]()
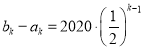 ,
,![]() ,
,
∵![]() ,
,![]() ,
,
![]()
![]() 時,
時,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() 時,
時,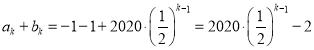 ,
,
![]()
![]() 時,
時,![]() 是單調(diào)遞減數(shù)列,
是單調(diào)遞減數(shù)列,
![]()
![]() 是滿足
是滿足![]() 的最大整數(shù),
的最大整數(shù),
![]()
![]() 時,
時,![]() 恒成立;
恒成立;![]() 時,
時,![]() ,
,![]() ,
,
![]()
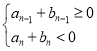 ,
,
即 ,
,
解得![]() ,
,
![]()
![]() 為正整數(shù),
為正整數(shù),![]() ,
,
![]()
![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩人2013-2017這五年的年度體檢的血壓值的折線圖如圖所示.

(1)根據(jù)散點(diǎn)圖,直接判斷甲、乙這五年年度體檢的血壓值誰的波動更大,并求波動更大者的方差;
(2)根據(jù)乙這五年年度體檢血壓值的數(shù)據(jù),求年度體檢血壓值![]() 關(guān)于年份
關(guān)于年份![]() 的線性回歸方程,并據(jù)此估計乙在2018年年度體檢的血壓值.
的線性回歸方程,并據(jù)此估計乙在2018年年度體檢的血壓值.
(附: ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,某鎮(zhèn)有一塊空地![]() ,其中
,其中![]() ,
,![]() ,
,![]() .當(dāng)?shù)劓?zhèn)政府規(guī)劃將這塊空地改造成一個旅游景點(diǎn),擬在中間挖一個人工湖
.當(dāng)?shù)劓?zhèn)政府規(guī)劃將這塊空地改造成一個旅游景點(diǎn),擬在中間挖一個人工湖![]() ,其中
,其中![]() ,
,![]() 都在邊
都在邊![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地帶上形成假山,剩下的
地帶上形成假山,剩下的![]() 地帶開設(shè)兒童游樂場.為安全起見,需在
地帶開設(shè)兒童游樂場.為安全起見,需在![]() 的周圍安裝防護(hù)網(wǎng).
的周圍安裝防護(hù)網(wǎng).

(1)當(dāng)![]() 時,求防護(hù)網(wǎng)的總長度;
時,求防護(hù)網(wǎng)的總長度;
(2)為節(jié)省投入資金,人工湖![]() 的面積要盡可能小,問如何設(shè)計施工方案,可使
的面積要盡可能小,問如何設(shè)計施工方案,可使![]() 的面積最小?最小面積是多少?
的面積最小?最小面積是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
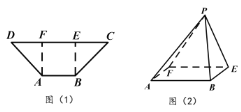
【題目】如圖(1),等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分別是
分別是![]() 的兩個三等分點(diǎn).若把等腰梯形沿虛線
的兩個三等分點(diǎn).若把等腰梯形沿虛線![]() 、
、![]() 折起,使得點(diǎn)
折起,使得點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 重合,記為點(diǎn)
重合,記為點(diǎn)![]() ,如圖(2).
,如圖(2).
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】有一種候鳥每年都按一定的路線遷陟,飛往繁殖地產(chǎn)卵.科學(xué)家經(jīng)過測量發(fā)現(xiàn)候鳥的飛行速度可以表示為函數(shù)![]() ,單位是
,單位是![]() ,其中
,其中![]() 表示候鳥每分鐘耗氧量的單位數(shù),
表示候鳥每分鐘耗氧量的單位數(shù),![]() 表示測量過程中候鳥每分鐘的耗氧偏差.(參考數(shù)據(jù):
表示測量過程中候鳥每分鐘的耗氧偏差.(參考數(shù)據(jù):![]() ,
,![]() ,
,![]() )
)
(1)若![]() ,候鳥每分鐘的耗氧量為
,候鳥每分鐘的耗氧量為![]() 個單位時,它的飛行速度是多少
個單位時,它的飛行速度是多少![]() ?
?
(2)若![]() ,候鳥停下休息時,它每分鐘的耗氧量為多少個單位?
,候鳥停下休息時,它每分鐘的耗氧量為多少個單位?
(3)若雄鳥的飛行速度為![]() ,雌鳥的飛行速度為
,雌鳥的飛行速度為![]() ,那么此時雄鳥每分鐘的耗氧量是雌鳥每分鐘的耗氧量的多少倍?
,那么此時雄鳥每分鐘的耗氧量是雌鳥每分鐘的耗氧量的多少倍?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左
的左![]() 、
、![]() 右焦點(diǎn)分別為,點(diǎn)
右焦點(diǎn)分別為,點(diǎn)![]() 在橢圓上,且滿足
在橢圓上,且滿足![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)傾斜角為![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點(diǎn),記
兩點(diǎn),記![]() 的面積為
的面積為![]() ,求
,求![]() 取最大值時直線
取最大值時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)![]()
(1)若函數(shù)在區(qū)間![]() 上存在零點(diǎn),求實數(shù)
上存在零點(diǎn),求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)是否存在常數(shù)![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() 的值域為區(qū)間
的值域為區(qū)間![]() ,且區(qū)間
,且區(qū)間![]() 的長度為
的長度為![]() (視區(qū)間
(視區(qū)間![]() 的長度為
的長度為![]() ),如果存在,求出
),如果存在,求出![]() 的值;如果不存在,說明理由.
的值;如果不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
,![]() ,
,![]() ,記
,記![]() .
.
(1)求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)當(dāng)![]() 時,若函數(shù)
時,若函數(shù)![]() 沒有零點(diǎn),求
沒有零點(diǎn),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com