
【題目】下列命題錯誤的個數是( )
①在![]() 中,
中,![]() 是
是![]() 的充要條件;
的充要條件;
②若向量![]() 滿足
滿足![]() ,則
,則![]() 與
與![]() 的夾角為鈍角;
的夾角為鈍角;
③若數列![]() 的前
的前![]() 項和
項和![]() ,則數列
,則數列![]() 為等差數列;
為等差數列;
④若![]() ,則“
,則“![]() ”是“
”是“![]() ”的必要不充分條件.
”的必要不充分條件.
A.1B.2C.3D.4
【答案】A
【解析】
對于①,在![]() 中,由正弦定理
中,由正弦定理![]() 可得,
可得,![]() 是
是![]() 的充要條件;
的充要條件;
對于②,若向量![]() 滿足
滿足![]() ,則
,則![]() 與
與![]() 的夾角為鈍角或
的夾角為鈍角或![]() 與
與![]() 反向共線;
反向共線;
對于③,由已知可得![]() ,則數列
,則數列![]() 為等差數列;
為等差數列;
對于④,由“![]() ”的充要條件為 “
”的充要條件為 “![]() 或
或![]() ”,再判斷即可得解.
”,再判斷即可得解.
解:對于①,在![]() 中,由正弦定理
中,由正弦定理![]() ,則
,則![]() 的充要條件為
的充要條件為![]() ,由三角形的性質可得
,由三角形的性質可得![]() 的充要條件為
的充要條件為![]() ,即在
,即在![]() 中,
中,![]() 是
是![]() 的充要條件,即①正確;
的充要條件,即①正確;
對于②,若向量![]() 滿足
滿足![]() ,則
,則![]() 與
與![]() 的夾角為鈍角或
的夾角為鈍角或![]() 與
與![]() 反向共線,即②錯誤;
反向共線,即②錯誤;
對于③,若數列![]() 的前
的前![]() 項和
項和![]() ,則當
,則當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() 滿足上式,即
滿足上式,即![]() ,則
,則![]() ,則數列
,則數列![]() 為等差數列,即③正確;
為等差數列,即③正確;
對于④,由“![]() ”的充要條件為“
”的充要條件為“![]() ”,即“
”,即“![]() 或
或![]() ”,又“
”,又“![]() 或
或![]() ”是“
”是“![]() ”的必要不充分條件,即“
”的必要不充分條件,即“![]() ”是“
”是“![]() ”的必要不充分條件,即④正確.
”的必要不充分條件,即④正確.
命題錯誤的個數是1個,
故選:A.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知三棱錐P-ABC(如圖一)的平面展開圖(如圖二)中,四邊形ABCD為邊長等于![]() 的正方形,
的正方形,![]() 和
和![]() 均為正三角形,在三棱錐P-ABC中:
均為正三角形,在三棱錐P-ABC中:
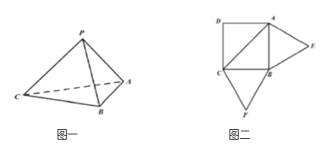
(1)證明:平面![]() 平面ABC;
平面ABC;
(2)若點M在棱PA上運動,當直線BM與平面PAC所成的角最大時,求直線MA與平面MBC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲同學參加化學競賽初賽,考試分為筆試、口試、實驗三個項目,各單項通過考試的概率依次為![]() 、
、![]() 、
、![]() ,筆試、口試、實驗通過考試分別記4分、2分、4分,沒通過的項目記0分,各項成績互不影響.
,筆試、口試、實驗通過考試分別記4分、2分、4分,沒通過的項目記0分,各項成績互不影響.
(Ⅰ)若規定總分不低于8分即可進入復賽,求甲同學進入復賽的概率;
(Ⅱ)記三個項目中通過考試的個數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,四邊形
,四邊形![]() 是菱形,
是菱形,![]() ,
,![]() ,且
,且![]() 交于點
交于點![]() ,
,![]() 是
是![]() 上任意一點.
上任意一點.
(1)求證![]() ;
;
(2)已知二面角![]() 的余弦值為
的余弦值為![]() ,若
,若![]() 為
為![]() 的中點,求
的中點,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為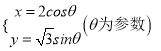 ,在同一平面直角坐標系中,將曲線
,在同一平面直角坐標系中,將曲線![]() 上的點按坐標變換
上的點按坐標變換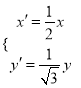 得到曲線
得到曲線![]() ,以原點為極點,
,以原點為極點, ![]() 軸的正半軸為極軸,建立極坐標系.
軸的正半軸為極軸,建立極坐標系.
(Ⅰ)求曲線![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)若過點![]() (極坐標)且傾斜角為
(極坐標)且傾斜角為![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,弦
兩點,弦![]() 的中點為
的中點為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
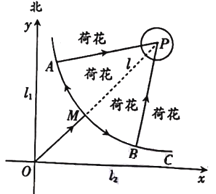
【題目】如圖,某市建有貫穿東西和南北的兩條垂直公路![]() ,
,![]() ,在它們交叉路口點
,在它們交叉路口點![]() 處的東北方向建有一個荷花池,荷花池的外圍是一條環形公路,荷花池中的固定觀景臺
處的東北方向建有一個荷花池,荷花池的外圍是一條環形公路,荷花池中的固定觀景臺![]() 位于兩條垂直公路的角平分線
位于兩條垂直公路的角平分線![]() 上,
上,![]() 與環形公路的交點記作
與環形公路的交點記作![]() .游客游覽荷花池時,需沿公路
.游客游覽荷花池時,需沿公路![]() 先到達環形公路
先到達環形公路![]() 處.為了分流游客,方便游客游覽荷花池,計劃從靠近公路
處.為了分流游客,方便游客游覽荷花池,計劃從靠近公路![]() ,
,![]() 的環形公路上選
的環形公路上選![]() ,
,![]() 兩處(
兩處(![]() ,
,![]() 關于直線
關于直線![]() 對稱)修建直達觀景臺
對稱)修建直達觀景臺![]() 的玻璃棧道
的玻璃棧道![]() ,
,![]() .以
.以![]() ,
,![]() 所在的直線為
所在的直線為![]() ,
,![]() 軸建立平面直角坐標系
軸建立平面直角坐標系![]() ,靠近公路
,靠近公路![]() ,
,![]() 的環形公路可用曲線
的環形公路可用曲線![]() 近似表示,曲線
近似表示,曲線![]() 符合函數
符合函數![]() .
.
(1)若![]() 百米,點
百米,點![]() 到
到![]() 的垂直距離為1百米,求玻璃棧道
的垂直距離為1百米,求玻璃棧道![]() 的總長度;
的總長度;
(2)若要使得玻璃棧道![]() 的總長度最小為
的總長度最小為![]() 百米,求觀景臺
百米,求觀景臺![]() 的位置.
的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是邊長為2的菱形,
是邊長為2的菱形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,點
,點![]() 為棱
為棱![]() 的中點.
的中點.

(Ⅰ)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ,并說明理由;
,并說明理由;
(Ⅱ)當二面角![]() 的余弦值為
的余弦值為![]() 時,求直線
時,求直線![]() 與平面
與平面![]() 所成的角.
所成的角.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com