
【題目】已知曲線C: ![]() =1(y≥0),直線l:y=kx+1與曲線C交于A,D兩點,A,D兩點在x軸上的射影分別為點B,C.記△OAD的面積S1 , 四邊形ABCD的面積為S2 . (Ⅰ)當點B坐標為(﹣1,0)時,求k的值;
=1(y≥0),直線l:y=kx+1與曲線C交于A,D兩點,A,D兩點在x軸上的射影分別為點B,C.記△OAD的面積S1 , 四邊形ABCD的面積為S2 . (Ⅰ)當點B坐標為(﹣1,0)時,求k的值;
(Ⅱ)若S1= ![]() ,求線段AD的長;
,求線段AD的長;
(Ⅲ)求 ![]() 的范圍.
的范圍.
【答案】解:(Ⅰ)由題意,y=kx+1與曲線C交于A,D兩點,A,D兩點在x軸上的射影分別為點B,C.點B坐標為(﹣1,0), 則點A的橫坐標為﹣1,代入曲線C: ![]() =1(y≥0),解得點A的縱坐標為x=
=1(y≥0),解得點A的縱坐標為x= ![]() ,
,
即A(﹣1, ![]() )
)
∵點A在直線y=kx+1,則有: ![]() =k×(﹣1)+1,
=k×(﹣1)+1,
∴解得k=﹣ ![]() ,
,
k的值﹣ ![]() ;
;
(Ⅱ)由題意,k不存在時,四邊形ABCD也不存在,則k必須存在.
設點A(xA , yA),點D(xD , yD),則點B(xA , 0),點C(xD , 0)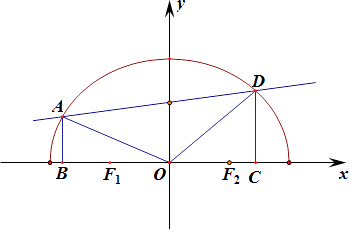
直線l:y=kx+1與曲線C交于A,D兩點,
A,D兩點代入曲線C,即 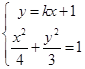 ,消去y,整理得:(3+4k2)x2+8kx﹣8=0,
,消去y,整理得:(3+4k2)x2+8kx﹣8=0,
由直線l經過橢圓左右頂點時,k=± ![]() ,
,
則﹣ ![]() ≤k≤
≤k≤ ![]() ,
,
解得:xA+xD=﹣ ![]() ,xAxD=
,xAxD= ![]() ,|AD|=
,|AD|= ![]() =
= 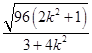 ,
,
△OAD的面積為S1 , 設原點(0,0)到直線l:y=kx+1距離為h,
則h= ![]() ,
,
S1= ![]() =
= ![]() |AD|h=
|AD|h= ![]() =
= ![]() ,整理得:40k4+11k2﹣2=0,則k2=
,整理得:40k4+11k2﹣2=0,則k2= ![]() ,
,
解得k=± ![]() ,|AD|=
,|AD|= ![]() ,
,
∴線段AD的長 ![]() ;
;
(Ⅲ)由題意及(i):可知:S2= ![]() (y1+y2)丨x1﹣x2丨,
(y1+y2)丨x1﹣x2丨,
則 ![]() =
=  =
= ![]() ,
,
由y1+y2=kx1+1+kx2+1=k(x1+x2)+2,
∴ ![]() =
= ![]() =
= 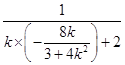 =
= ![]() ,
,
由﹣ ![]() ≤k≤
≤k≤ ![]() ,
,
∴ ![]() ≤
≤ ![]() ≤
≤ ![]() ,
,
∴ ![]() 的取值范圍[
的取值范圍[ ![]() ,
, ![]() ].
].
【解析】(Ⅰ)由題意B(﹣1,0),將x=﹣1代入橢圓方程,即可求得A點坐標,代入直線方程,即可求得k的值;(Ⅱ)將直線方程代入橢圓方程,由題意求得k的取值范圍,利用韋達定理及弦長公式求得丨AD丨,根據三角形的面積公式,即可求得k的值,求得丨AD丨,(Ⅲ)求得,四邊形ABCD的面積為S2 , 求得 ![]() 的表達式,由k的取值范圍,即可求得
的表達式,由k的取值范圍,即可求得 ![]() 的取值范圍.
的取值范圍.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥DC,AB⊥AD,AB=3,CD=2,PD=AD=5. 
(1)在PD上確定一點E,使得PB∥平面ACE,并求 ![]() 的值;
的值;
(2)在(1)條件下,求平面PAB與平面ACE所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+ ![]() ,現有一組數據,繪制得到莖葉圖,且莖葉圖中的數據的平均數為2.(莖葉圖中的數據均為小數,其中莖為整數部分,葉為小數部分)
,現有一組數據,繪制得到莖葉圖,且莖葉圖中的數據的平均數為2.(莖葉圖中的數據均為小數,其中莖為整數部分,葉為小數部分) 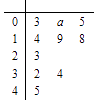
(Ⅰ)求a的值;
(Ⅱ)現從莖葉圖小于3的數據中任取2個數據分別替換m的值,求恰有1個數據使得函數f(x)沒有零點的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC和△A1B1C1滿足sinA=cosA1 , sinB=cosB1 , sinC=cosC1 .
(1)求證:△ABC是鈍角三角形,并求最大角的度數;
(2)求sin2A+sin2B+sin2C的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,數列{bn}滿足:bn+1=2bn+2,且an+1﹣an=bn;
,數列{bn}滿足:bn+1=2bn+2,且an+1﹣an=bn;
(1)求證:數列{bn+2}是等比數列;
(2)求數列{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的部分圖象如圖所示:
的部分圖象如圖所示:

(I)求![]() 的解析式及對稱中心坐標;
的解析式及對稱中心坐標;
(Ⅱ)將![]() 的圖象向右平移
的圖象向右平移![]() 個單位,再將橫坐標伸長到原來的2倍,縱坐標不變,最后將圖象向上平移1個單位,得到函數
個單位,再將橫坐標伸長到原來的2倍,縱坐標不變,最后將圖象向上平移1個單位,得到函數![]() 的圖象,求函數
的圖象,求函數![]() 在
在![]() 上的單調區間及最值.
上的單調區間及最值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com