
【題目】已知數(shù)列![]() 的前
的前![]() 項積為
項積為![]() ,即
,即![]() .
.
(1)若數(shù)列![]() 為首項為2016,公比為
為首項為2016,公比為![]() 的等比數(shù)列,
的等比數(shù)列,
①求![]() 的表達(dá)式;②當(dāng)
的表達(dá)式;②當(dāng)![]() 為何值時,
為何值時, ![]() 取得最大值;
取得最大值;
(2)當(dāng)![]() 時,數(shù)列
時,數(shù)列![]() 都有
都有![]() 且
且![]() 成立,
成立,
求證: ![]() 為等比數(shù)列.
為等比數(shù)列.
【答案】(1)① ;②12;(2)見解析.
;②12;(2)見解析.
【解析】試題分析:
(1)①由題意知![]() ,則
,則![]() ,化簡可得結(jié)論;②記
,化簡可得結(jié)論;②記![]() ,
,![]() ,即
,即![]() ,
,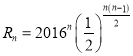 ,作商
,作商![]() ,計算出
,計算出![]() 的最大值,再由n是奇數(shù)時,
的最大值,再由n是奇數(shù)時, ![]() 負(fù)數(shù),n是偶數(shù)時,
負(fù)數(shù),n是偶數(shù)時, ![]() 是正數(shù),即可得出結(jié)論;
是正數(shù),即可得出結(jié)論;
(2) 當(dāng)![]() 時, 易得
時, 易得![]() ;由
;由![]() 得,當(dāng)
得,當(dāng)![]() 時,
時, ![]() ,兩式相除,化簡可得
,兩式相除,化簡可得![]() ,可得
,可得![]() ,這兩式相除,則易得結(jié)論.
,這兩式相除,則易得結(jié)論.
試題解析:
(1)①由題意知![]() ,
,
所以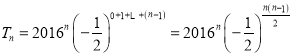
②記![]() ,
,![]() ,即
,即![]() ,
,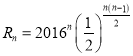 ,
,
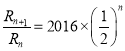 ,當(dāng)
,當(dāng)![]() 時,
時, ![]() ;當(dāng)
;當(dāng)![]() 時,
時, ![]() ,
,
又因為![]() ,所以,當(dāng)
,所以,當(dāng)![]() 時,
時, ![]() ;當(dāng)
;當(dāng)![]() 時,
時, ![]() ,所以
,所以![]() 的最大值為
的最大值為![]()
此時![]() ,而
,而![]() ,所以
,所以![]() .
.
而 ,
,
所以,當(dāng)![]() 時,
時, ![]() 取得最大值
取得最大值
(2)當(dāng)![]() 時,
時, ![]() ,所以
,所以![]() ,即
,即![]() ,
,
已知![]() ①
①
當(dāng)![]() 時,
時, ![]()
①②兩式相除得![]() ,化簡得
,化簡得![]() ,③
,③
又因為![]() ,④
,④
③兩式相除得![]() ,⑤
,⑤
⑤式可化為: 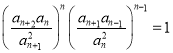 ,
, ![]()
令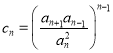 ,所以
,所以![]() ,所以
,所以![]() ,
,
即![]() ,
,![]() 都成立,
都成立,
所以![]() 為等比數(shù)列.
為等比數(shù)列.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)A,B為曲線C:y=![]() 上兩點(diǎn),A與B的橫坐標(biāo)之和為4.
上兩點(diǎn),A與B的橫坐標(biāo)之和為4.
(1)求直線AB的斜率;
(2)設(shè)M為曲線C上一點(diǎn),C在M處的切線與直線AB平行,且AM![]() BM,求直線AB的方程.
BM,求直線AB的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如下圖,在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的正方形,平面
的正方形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 為
為![]() 中點(diǎn),且
中點(diǎn),且![]() .
.
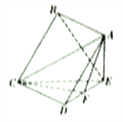
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求證: ![]() ;
;
(Ⅲ)求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)y=f(x)是定義在R上的增函數(shù),函數(shù)y=f(x﹣1)的圖象關(guān)于(1,0)對稱.若對任意的x,y∈R,不等式f(x2﹣6x+21)+f(y2﹣8y)<0恒成立,則當(dāng)x>3時,x2+y2的取值范圍是( )
A.(9,25)
B.(13,49)
C.(3,7)
D.(9,49)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,四邊形
,四邊形![]() 是直角梯形,
是直角梯形,![]() .
.
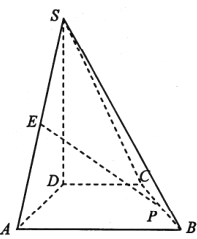
(1)求二面角![]() 的余弦值;
的余弦值;
(2)設(shè)![]() 是棱
是棱![]() 上一點(diǎn),
上一點(diǎn),![]() 是
是![]() 的中點(diǎn),若
的中點(diǎn),若![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了得到函數(shù)y=sin2x的圖象,只需把函數(shù)y=sin(2x﹣ ![]() )的圖象( )
)的圖象( )
A.向左平移 ![]() 個單位長度
個單位長度
B.向右平移 ![]() 個單位長度
個單位長度
C.向左平移 ![]() 個單位長度
個單位長度
D.向右平移 ![]() 個單位長度
個單位長度
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲罐中有4個紅球,3個白球和3個黑球;乙罐中有5個紅球,3個白球和2個黑球.先從甲罐中隨機(jī)取出一球放入乙罐,分別以A1、A2和A3表示由甲罐取出的球是紅球,白球和黑球的事件;再從乙罐中隨機(jī)取出一球,以B表示由乙罐取出的球是紅球的事件,下列的結(jié)論:
①P(B)= ![]() ;
;
②P(B|A1)= ![]() ;
;
③事件B與事件A1不相互獨(dú)立;
④A1 , A2 , A3是兩兩互斥的事件;
⑤P(B)的值不能確定,因為它與A1 , A2 , A3中哪一個發(fā)生有關(guān),
其中正確結(jié)論的序號為 . (把正確結(jié)論的序號都填上)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為宣傳3月5日學(xué)雷鋒紀(jì)念日,重慶二外在高一,高二年級中舉行學(xué)雷鋒知識競賽,每年級出3人組成甲乙兩支代表隊,首輪比賽每人一道必答題,答對則為本隊得1分,答錯不答都得0分,已知甲隊3人每人答對的概率分別為![]() ,乙隊每人答對的概率都是
,乙隊每人答對的概率都是![]() .設(shè)每人回答正確與否相互之間沒有影響,用
.設(shè)每人回答正確與否相互之間沒有影響,用![]() 表示甲隊總得分.
表示甲隊總得分.
(1)求隨機(jī)變量![]() 的分布列及其數(shù)學(xué)期望
的分布列及其數(shù)學(xué)期望![]() ;
;
(2)求甲隊和乙隊得分之和為4的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com