【題目】設拋物線
：
上一點
到焦點
的距離為5．
（1）求拋物線的方程；
（2）過點
的直線
與拋物線交于
兩點, 過點
作直線
的垂線，垂足為
，判斷：
三點是否共線，并說明理由．
【答案】（1）
；（2）
三點共線，理由見解析
【解析】
（1）解法一，利用焦半徑公式直接求得
值，解法二，根據點在拋物線上和兩點間的距離，列方程組求解；（2）解法一，分直線
的斜率不存在和存在兩種情況，斜率不存在時
和斜率存在時，利用直線方程和拋物線方程聯立，得到根與系數的關系驗證，說明三點共線，解法二，設直線
與拋物線方程聯立，利用
說明三點共線，解法三，設直線與拋物線方程聯立，利用
，說明三點共線.
（1）解法1: 由已知得
，
，
拋物線
的方程為
解法2: 由已知得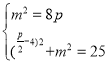
解得
或
又
拋物線的方程為
（2）解法1: 易知直線的斜率為0時. 直線與拋物線交于一點,不合題意.
(1)當直線的斜率不存在時，則
, 
,
.
,
三點共線
(2)當直線的斜率存在時，設：
.
,消
整理得
設
,
,則
.
,
三點共線.
綜上(1) (2)知三點共線
（2）解法2: 易知直線的斜率為0時. 直線與拋物線交于一點,不合題意.
可設直線.
由
,得
.
設，則
則
, 
又
,
三點共線
（2）解法3: 易知直線的斜率為0時. 直線與拋物線交于一點,不合題意.
可設直線.
由,得.
設，則
則,
又
有公共點
,
三點共線
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】某校高二年級共有800名學生參加了數學測驗（滿分150分），已知這800名學生的數學成績均不低于90分，將這800名學生的數學成績分組如：
，
，
，
，
，得到的頻率分布直方圖如圖所示，則下列說法中正確的是( )
①
；②這800名學生中數學成績在110分以下的人數為160； ③這800名學生數學成績的中位數約為121.4；④這800名學生數學成績的平均數為125.
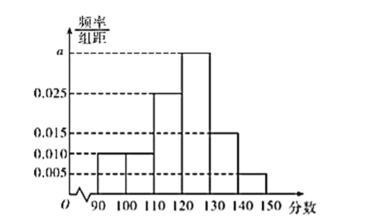
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，橢圓W：
的焦距與橢圓Ω：
+y2＝1的短軸長相等，且W與Ω的長軸長相等，這兩個橢圓的在第一象限的交點為A，直線l經過Ω在y軸正半軸上的頂點B且與直線OA（O為坐標原點）垂直，l與Ω的另一個交點為C，l與W交于M，N兩點．
（1）求W的標準方程：
（2）求
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列三個命題：
①函數
的單調增區間是
②經過任意兩點的直線，都可以用方程
來表示；
③命題
：“
，
”的否定是“
，
”，
其中正確命題的個數有（ ）個
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f(x)＝|x－a|.
(1)當a＝2時，解不等式f(x)≥4－|x－1|；
(2)若f(x)≤1的解集為[0,2]，
(m>0，n>0)，求證：m＋2n≥4.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱
中，各個側面均是邊長為
的正方形，
為線段
的中點
（Ⅰ）求證：
⊥平面
；
（Ⅱ）求證：直線
∥平面
；
（Ⅲ）設
為線段
上任意一點，在
內的平面區域（包括邊界）是否存在點
，使
，并說明理由
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P-ABCD中，AB//CD，且
（1）證明：平面PAB⊥平面PAD；
（2）若PA=PD=AB=DC, 
,且四棱錐P-ABCD的體積為
，求該四棱錐的側面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
