Question

【題目】已知函數.

（1）完成表一中對應的值，并在坐標系中用描點法作出函數的圖象：（表一）

	0.25	0.5	0.75	1	1.25	1.5
			0.08		1.82	2.58

（2）根據你所作圖象判斷函數的單調性，并用定義證明；

（3）說明方程的根在區間存在的理由，并從表二中求使方程的根的近似值達到精確度為0.01時運算次數的最小值并求此時方程的根的近似值，且說明理由.

（表二）二分法的結果

運算次數的值		左端點	右端點
	-0.537	0.6	0.75	0.08
	-0.217	0.675	0.75	0.08
	-0.064	0.7125	0.75	0.08
	-0.064	0.7125	0.73125	0.011
	-0.03	0.721875	0.73125	0.011
	-0.01	0.7265625	0.73125	0.011

Answer 1

【答案】（1）見解析 （2）增函數，證明見解析 （3），方程的根的近似值為，理由見解析

【解析】

(1)分別代入表中的數據進行求解再描點即可.

(2)由圖像直觀判斷即可.再設區間內,判斷的正負進行證明即可.

(3)根據零點存在性定理證明即可證明程的根在區間存在.再根據圖表判斷當根的近似值與的差的絕對值小于時的最小值即可.

解：（1）

		0.5	0.75	1	1.25	1.5
			0.08	1	1.82	2.58

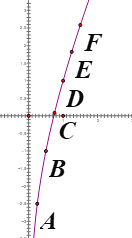
（2）函數在定義域內為增函數,證明：設,則,,因為

即所以函數在定義域內為增函數.

（3）是圖象是一條連續不斷的曲線,

且,故方程的根在區間存在.

當時,所以當時方程的根的近似值達不到精確度為0.01,

當時,所以當時方程的根的近似值達到精確度為0.01,所以.

方程的根的近似值為.