
【題目】已知函數![]() (
(![]() )且函數
)且函數![]() 是奇函數.
是奇函數.
(1)求![]() 的值;
的值;
(2)是否存在這樣的實數![]() ,使
,使![]() 對所有的
對所有的![]() 均成立?若存在,求出適合條件的實數
均成立?若存在,求出適合條件的實數![]() 的值或范圍;若不存在,說明理由.
的值或范圍;若不存在,說明理由.
 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案科目:高中數學 來源: 題型:
【題目】如圖,![]() ,
,![]() ,
,![]() 是同一平面內的三條平行直線,
是同一平面內的三條平行直線, ![]() 與
與![]() 之間的距離是1,
之間的距離是1,![]() 與
與![]() 之間的距離是2,三角形
之間的距離是2,三角形![]() 的三個頂點分別在
的三個頂點分別在![]() ,
,![]() ,
,![]() 上.
上.
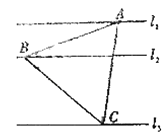
(1)若![]() 為正三角形,求其邊長;
為正三角形,求其邊長;
(2)若![]() 是以B為直角頂點的直角三角形,求其面積的最小值.
是以B為直角頂點的直角三角形,求其面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)完成表一中![]() 對應的
對應的![]() 值,并在坐標系中用描點法作出函數
值,并在坐標系中用描點法作出函數![]() 的圖象:(表一)
的圖象:(表一)
| 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.5 |
| 0.08 | 1.82 | 2.58 |
(2)根據你所作圖象判斷函數![]() 的單調性,并用定義證明;
的單調性,并用定義證明;
(3)說明方程![]() 的根在區間
的根在區間![]() 存在的理由,并從表二中求使方程
存在的理由,并從表二中求使方程![]() 的根的近似值達到精確度為0.01時運算次數
的根的近似值達到精確度為0.01時運算次數![]() 的最小值并求此時方程
的最小值并求此時方程![]() 的根的近似值,且說明理由.
的根的近似值,且說明理由.
(表二)二分法的結果
運算次數 |
| 左端點 | 右端點 |
|
| -0.537 | 0.6 | 0.75 | 0.08 |
| -0.217 | 0.675 | 0.75 | 0.08 |
| -0.064 | 0.7125 | 0.75 | 0.08 |
| -0.064 | 0.7125 | 0.73125 | 0.011 |
| -0.03 | 0.721875 | 0.73125 | 0.011 |
| -0.01 | 0.7265625 | 0.73125 | 0.011 |
查看答案和解析>>
科目:高中數學 來源: 題型:
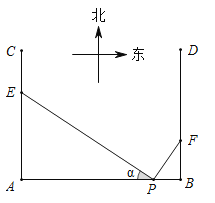
【題目】如圖,在P地正西方向8km的A處和正東方向1km的B處各有一條正北方向的公路AC和BD,現計劃在AC和BD路邊各修建一個物流中心E和F,為緩解交通壓力,決定修建兩條互相垂直的公路PE和PF,設![]()
![]() Ⅰ
Ⅰ![]() 為減少對周邊區域的影響,試確定E,F的位置,使
為減少對周邊區域的影響,試確定E,F的位置,使![]() 與
與![]() 的面積之和最小;
的面積之和最小;
![]() Ⅱ
Ⅱ![]() 為節省建設成本,求使
為節省建設成本,求使![]() 的值最小時AE和BF的值.
的值最小時AE和BF的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,
,![]() 為
為![]() 軸上的點.
軸上的點.
(1)過點![]() 作直線
作直線![]() 與
與![]() 相切,求切線
相切,求切線![]() 的方程;
的方程;
(2)如果存在過點![]() 的直線
的直線![]() 與拋物線交于
與拋物線交于![]() ,
,![]() 兩點,且直線
兩點,且直線![]() 與
與![]() 的傾斜角互補,求實數
的傾斜角互補,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為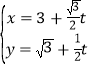 (
(![]() 為參數),點
為參數),點![]() 的極坐標為
的極坐標為![]() ,設直線
,設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別為![]() ,已知
,已知![]() 且
且![]() .
.
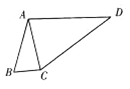
(1)求角![]() ;
;
(2)如圖,D為△ABC外一點,若在平面四邊形ABCD中,![]() ,求△ACD面積的最大值.
,求△ACD面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
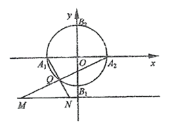
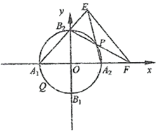
【題目】在平面直角坐標系xOy中,圓O:![]() 與坐標軸分別交于A1,A2,B1,B2(如圖).
與坐標軸分別交于A1,A2,B1,B2(如圖).
(1)點Q是圓O上除A1,A2外的任意點(如圖1),直線A1Q,A2Q與直線![]() 交于不同的兩點M,N,求線段MN長的最小值;
交于不同的兩點M,N,求線段MN長的最小值;
(2)點P是圓O上除A1,A2,B1,B2外的任意點(如圖2),直線B2P交x軸于點F,直線A1B2交A2P于點E.設A2P的斜率為k,EF的斜率為m,求證:2m﹣k為定值.
(圖1) (圖2)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com