
【題目】函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)當![]() 時,方程
時,方程![]() 在區間
在區間![]() 內有唯一實數解,求實數
內有唯一實數解,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2) ![]() 或
或![]()
【解析】
(1)先求得函數![]() 的導函數和定義域,對
的導函數和定義域,對![]() 分成
分成![]() 等
等![]() 種情況,分類討論函數的單調性.(2)將
種情況,分類討論函數的單調性.(2)將![]() 分離常數化為
分離常數化為![]() ,構造函數
,構造函數![]() ,利用導數求得
,利用導數求得![]() 的單調性和最值,由此求得
的單調性和最值,由此求得![]() 的取值范圍.
的取值范圍.
(1)![]() ,
,
(i)當![]() 時,
時,![]() ,令
,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
函數![]() 在
在![]() 上單調遞增,
上單調遞增,![]() 上單調遞減;
上單調遞減;
(ii)當![]() 時,令
時,令![]() ,得
,得![]() ,
,![]()
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
函數![]() 在
在![]() 和
和![]() 上單調遞增,
上單調遞增,![]() 上單調遞減;
上單調遞減;
(iii)當![]() 時,
時,![]() ,函數f(x)在
,函數f(x)在![]() 上單調遞增;
上單調遞增;
(iv)當![]() 時,
時,![]()
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]()
函數![]() 在
在![]() 和
和![]() 上單調遞增,
上單調遞增,![]() 上單調遞減;
上單調遞減;
綜上所述:當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;
當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() 和
和![]() ,單調遞減區間為
,單調遞減區間為![]() ;
;
當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ;
;
當![]() 時,函數
時,函數![]() 的單調遞增區間為
的單調遞增區間為![]() 和
和![]() ,單調遞減區間為
,單調遞減區間為![]()
(2)當![]() 時,
時,![]() ,由
,由![]() ,得
,得![]() ,
,
又![]() ,所以
,所以![]() ,要使方程
,要使方程![]() 在區間
在區間![]() 上有唯一實數解,
上有唯一實數解,
只需![]() 有唯一實數解,
有唯一實數解,
令![]() ,∴
,∴![]() ,
,
由![]() 得
得![]() ;
;![]() 得
得![]() ,
,
∴![]() 在區間
在區間![]() 上是增函數,在區間
上是增函數,在區間![]() 上是減函數.
上是減函數.
![]() ,
,![]() ,
,![]() ,故
,故![]() 或
或![]()


科目:高中數學 來源: 題型:
【題目】對于由2n個質數組成的集合![]() ,可將其元素兩兩搭配成n個乘積,得到一個n元集.若
,可將其元素兩兩搭配成n個乘積,得到一個n元集.若![]() 與
與![]() 是由此得到的兩個n元集,其中,
是由此得到的兩個n元集,其中, ![]() ,且
,且![]() ,則稱集合對{A ,B}是由M炮制成的一幅“對聯”(如由四元集{a,b,c,d}可炮制成三幅對聯:
,則稱集合對{A ,B}是由M炮制成的一幅“對聯”(如由四元集{a,b,c,d}可炮制成三幅對聯:
![]()
![]() .
.
求六元質數集M={a,b,c,d,e,f}所能炮制成的對聯數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 指數是用體重公斤數除以身高米數的平方得出的數字,是國際上常用的衡量人體胖瘦程度以及是否健康的一個標準.對于高中男體育特長生而言,當
指數是用體重公斤數除以身高米數的平方得出的數字,是國際上常用的衡量人體胖瘦程度以及是否健康的一個標準.對于高中男體育特長生而言,當![]() 數值大于或等于20.5時,我們說體重較重,當
數值大于或等于20.5時,我們說體重較重,當![]() 數值小于20.5時,我們說體重較輕,身高大于或等于
數值小于20.5時,我們說體重較輕,身高大于或等于![]() 我們說身高較高,身高小于170cm我們說身高較矮.
我們說身高較高,身高小于170cm我們說身高較矮.
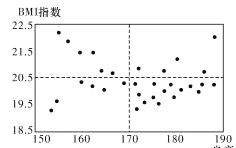
(1)已知某高中共有32名男體育特長生,其身高與![]() 指數的數據如散點圖,請根據所得信息,完成下述列聯表,并判斷是否有
指數的數據如散點圖,請根據所得信息,完成下述列聯表,并判斷是否有![]() 的把握認為男生的身高對
的把握認為男生的身高對![]() 指數有影響.
指數有影響.
身高較矮 | 身高較高 | 合計 | |
體重較輕 | |||
體重較重 | |||
合計 |
(2)①從上述32名男體育特長生中隨機選取8名,其身高和體重的數據如表所示:
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
體重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根據最小二乘法的思想與公式求得線性回歸方程為![]() .利用已經求得的線性回歸方程,請完善下列殘差表,并求解釋變量(身高)對于預報變量(體重)變化的貢獻值(保留兩位有效數字)
.利用已經求得的線性回歸方程,請完善下列殘差表,并求解釋變量(身高)對于預報變量(體重)變化的貢獻值(保留兩位有效數字)![]() ;
;
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
體重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
殘差 | 0.1 | 0.3 | 0.9 |
|
|
②通過殘差分析,對于殘差的最大(絕對值)的那組數據,需要確認在樣本點的采集中是否有人為的錯誤,已知通過重新采集發現,該組數據的體重應該為![]() .請重新根據最最小二乘法的思想與公式,求出男體育特長生的身高與體重的線性回歸方程.
.請重新根據最最小二乘法的思想與公式,求出男體育特長生的身高與體重的線性回歸方程.
(參考公式)
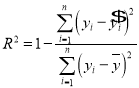 ,
,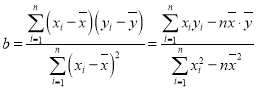 ,
,![]() ,
,![]() ,
,![]() .
.
(參考數據)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
0.10
0.05
0.01
0.005
![]()
2.706
3.811
6.635
7.879
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 為拋物線
為拋物線![]() :
:![]() 的焦點,拋物線
的焦點,拋物線![]() 上的點
上的點![]() 滿足
滿足![]() (
(![]() 為坐標原點),且
為坐標原點),且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)若直線![]() :
:![]() 與拋物線
與拋物線![]() 交于不同的兩點
交于不同的兩點![]() ,是否存在實數
,是否存在實數![]() 及定點
及定點![]() ,對任意實數
,對任意實數![]() ,都有
,都有![]() ?若存在,求出
?若存在,求出![]() 的值及點
的值及點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為維護交通秩序,防范電動自行車被盜,天津市公安局決定,開展二輪電動自行車免費登記、上牌照工作.電動自行車牌照分免費和收費(安裝防盜裝置)兩大類,群眾可以 自愿選擇安裝.已知甲、乙、丙三個不同類型小區的人數分別為15000,15000,20000.交管部門為了解社區居民意愿,現采用分層抽樣的方法從中抽取10人進行電話訪談.
(Ⅰ)應從甲小區和丙小區的居民中分別抽取多少人?
(Ⅱ)設從甲小區抽取的居民為![]() ,丙小區抽取的居民為
,丙小區抽取的居民為![]() .現從甲小區和丙小區已抽取的居民中隨機抽取2人接受問卷調查.
.現從甲小區和丙小區已抽取的居民中隨機抽取2人接受問卷調查.
(ⅰ)試用所給字母列舉出所有可能的抽取結果;
(ⅱ)設![]() 為事件“抽取的2人來自不同的小區”,求事件
為事件“抽取的2人來自不同的小區”,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將高二(1)班的四個同學分到語文、數學、英語三個興趣小組,每個興趣小組至少有一名同學的分配方法有多少種?下列結論正確的有( )
A.![]() B.
B.![]()
C.![]() D.18
D.18
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com