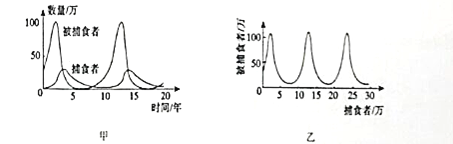
【題目】圖甲中的兩條曲線分別表示某理想狀態下捕食者和被捕食者數量隨時間的變化規律、對捕食者和被捕食者數量之間的關系描述錯誤的是（ ）
A. 捕食者和被捕食者數量與時間以
年為周期
B. 由圖可知，當捕食者數量增多的過程中，被捕食者數量先增多后減少
C. 捕食者和被捕食者數量之間的關系可以用圖1乙描述
D. 捕食者的數量在第
年和
年之間數量在急速減少
每日10分鐘口算心算速算天天練系列答案科目：高中數學 來源： 題型：
【題目】某公司共有60位員工，為提高員工的業務技術水平，公司擬聘請專業培訓機構進行培訓．培訓的總費用由兩部分組成：一部分是給每位參加員工支付400元的培訓材料費；另一部分是給培訓機構繳納的培訓費．若參加培訓的員工人數不超過30人，則每人收取培訓費1000元；若參加培訓的員工人數超過30人，則每超過1人，人均培訓費減少20元．設公司參加培訓的員工人數為x人，此次培訓的總費用為y元．
（1）求出y與x之間的函數關系式；
（2）請你預算：公司此次培訓的總費用最多需要多少元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖：已知四棱錐P—ABCD的底面ABCD是平行四邊形，PA⊥面ABCD，M是AD的中點，N是PC的中點.
（1）求證：MN∥面PAB；
（2）若平面PMC⊥面PAD，求證：CM⊥AD.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某品牌汽車的
店，對最近100份分期付款購車情況進行統計，統計情況如下表所示.已知分9期付款的頻率為0.4；該店經銷一輛該品牌汽車，若顧客分3期付款，其利潤為1萬元；分6期或9期付款，其利潤為2萬元；分12期付款，其利潤為3萬元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
頻數 | 20 | 20 |
|
|
（1）若以上表計算出的頻率近似替代概率，從該店采用分期付款購車的顧客（數量較大）中隨機抽取3為顧客，求事件
：“至多有1位采用分6期付款“的概率
；
（2）按分層抽樣方式從這100為顧客中抽取5人，再從抽取的5人中隨機抽取3人，記該店在這3人身上賺取的總利潤為隨機變量
，求
的分布列和數學期望
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱柱
中，
平面
，
，
，
，
為棱
上一動點，過直線
的平面分別與棱
，
交于點
，
，則下列結論正確的是__________．
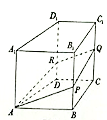
①對于任意的點，都有
②對于任意的點，四邊形
不可能為平行四邊形
③存在點，使得
為等腰直角三角形
④存在點，使得直線
平面
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校高二年級舉辦了一次數學史知識競賽活動，共有
名學生參加了這次競賽．為了解本次競賽的成績情況，從中抽取了部分學生的成績（得分均為整數，滿分為
分）進行統計，統計結果見下表．請你根據頻率分布表解答下列問題：
（1）填出頻率分布表中的空格；
（2）為鼓勵更多的學生了解“數學史”知識，成績不低于
分的同學能獲獎，請估計在參加的名學生中大概有多少名學生獲獎？
（3）在上述統計數據的分析中有一項計算見算法流程圖，求輸出的
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校有高三文科學生1000人，統計其高三上期期中考試的數學成績，得到頻率分布直方圖如下：
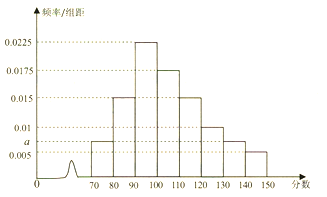
（1）求出圖中
的值，并估計本次考試低于120分的人數；
（2）假設同組的每個數據可用該組區間的中點值代替，試估計本次考試不低于120分的同學的平均數（其結果保留一位小數）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某品牌汽車的
店，對最近100份分期付款購車情況進行統計，統計情況如下表所示.已知分9期付款的頻率為0.4；該店經銷一輛該品牌汽車，若顧客分3期付款，其利潤為1萬元；分6期或9期付款，其利潤為2萬元；分12期付款，其利潤為3萬元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
頻數 | 20 | 20 |
|
|
（1）若以上表計算出的頻率近似替代概率，從該店采用分期付款購車的顧客（數量較大）中隨機抽取3為顧客，求事件
：“至多有1位采用分6期付款“的概率
；
（2）按分層抽樣方式從這100為顧客中抽取5人，再從抽取的5人中隨機抽取3人，記該店在這3人身上賺取的總利潤為隨機變量
，求
的分布列和數學期望
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
