
【題目】如圖所示,異面直線![]() ,
,![]() 互相垂直,
互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,截面
,截面![]() 分別與
分別與![]() ,
,![]() ,
,![]() ,
,![]() 相交于點
相交于點![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
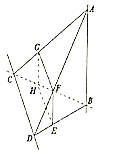
(1)求證:![]() 平面
平面![]() ;
;
(2)求銳二面角![]() 的正切值.
的正切值.
【答案】(1)見解析(2)![]()
【解析】分析:(1)推導出AB∥EF,CD∥HE,AB⊥BC,BC⊥DC,BC⊥EF,BC⊥EH,由此能證明BC⊥平面EFGH.
(2)作![]() ,以C為原點,CD為x軸,CB為y軸,Cz為z軸,建立空間直角坐標系C﹣xyz,利用向量法能求出二面角B﹣AD﹣C的正切值.
,以C為原點,CD為x軸,CB為y軸,Cz為z軸,建立空間直角坐標系C﹣xyz,利用向量法能求出二面角B﹣AD﹣C的正切值.
詳解:(1)∵![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
∴![]() ,同理
,同理![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() .
.
同理![]() .
.
∴![]() ,同理
,同理![]() .
.
又∵![]() ,
,![]() 是平面
是平面![]() 內的兩相交直線.
內的兩相交直線.
∴![]() 平面
平面![]() .
.
(2)由(1)及異面直線![]() ,
,![]() 互相垂直知,直線
互相垂直知,直線![]() ,
,![]() ,
,![]() 兩兩垂直.
兩兩垂直.
作![]() ,以
,以![]() 為原點,
為原點,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,建立空間直角坐標系
軸,建立空間直角坐標系![]() ,如圖所示,
,如圖所示,
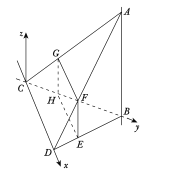
則![]() ,
,![]() ,
,![]() ,
,![]()
∵![]() 軸
軸![]() 平面
平面![]() ,∴平面
,∴平面![]() 的一個法向量可設為
的一個法向量可設為![]() ,
,
∵![]() ,∴
,∴![]() .
.
得![]() ,即
,即![]() ,
,
又∵![]() 軸
軸![]() 平面
平面![]() ,∴平面
,∴平面![]() 的一個法向量可設為
的一個法向量可設為![]() .
.
∴![]() ,得
,得![]() ,即
,即![]() ,
,
設銳二面角![]() 的大小為
的大小為![]() ,
,
那么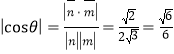 ,
,
∴![]()
∴二面角![]() 的正切值為
的正切值為![]() .
.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:高中數學 來源: 題型:
【題目】給出定義:若![]() (其中
(其中![]() 為整數),則
為整數),則![]() 叫做離實數
叫做離實數![]() 最近的整數,記作
最近的整數,記作![]() ,即
,即![]() .設函數
.設函數![]() ,二次函數
,二次函數![]() ,若函數
,若函數![]() 與
與![]() 的圖象有且只有一個公共點,則
的圖象有且只有一個公共點,則![]() 的取值不可能是( )
的取值不可能是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
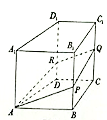
【題目】如圖,在四棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為棱
為棱![]() 上一動點,過直線
上一動點,過直線![]() 的平面分別與棱
的平面分別與棱![]() ,
,![]() 交于點
交于點![]() ,
,![]() ,則下列結論正確的是__________.
,則下列結論正確的是__________.
①對于任意的點![]() ,都有
,都有![]()
②對于任意的點![]() ,四邊形
,四邊形![]() 不可能為平行四邊形
不可能為平行四邊形
③存在點![]() ,使得
,使得![]() 為等腰直角三角形
為等腰直角三角形
④存在點![]() ,使得直線
,使得直線![]() 平面
平面![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校高二年級舉辦了一次數學史知識競賽活動,共有![]() 名學生參加了這次競賽.為了解本次競賽的成績情況,從中抽取了部分學生的成績(得分均為整數,滿分為
名學生參加了這次競賽.為了解本次競賽的成績情況,從中抽取了部分學生的成績(得分均為整數,滿分為![]() 分)進行統計,統計結果見下表.請你根據頻率分布表解答下列問題:
分)進行統計,統計結果見下表.請你根據頻率分布表解答下列問題:

(1)填出頻率分布表中的空格;
(2)為鼓勵更多的學生了解“數學史”知識,成績不低于![]() 分的同學能獲獎,請估計在參加的
分的同學能獲獎,請估計在參加的![]() 名學生中大概有多少名學生獲獎?
名學生中大概有多少名學生獲獎?
(3)在上述統計數據的分析中有一項計算見算法流程圖,求輸出的![]() 的值.
的值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市根據地理位置劃分成了南北兩區,為調查該市的一種經濟作物![]() (下簡稱
(下簡稱![]() 作物)的生長狀況,用簡單隨機抽樣方法從該市調查了 500 處
作物)的生長狀況,用簡單隨機抽樣方法從該市調查了 500 處 ![]() 作物種植點,其生長狀況如表:
作物種植點,其生長狀況如表:

其中生長指數的含義是:2 代表“生長良好”,1 代表“生長基本良好”,0 代表“不良好,但仍有收成”,﹣1代表“不良好,絕收”.
(1)估計該市空氣質量差的![]() 作物種植點中,不絕收的種植點所占的比例;
作物種植點中,不絕收的種植點所占的比例;
(2)能否有 99%的把握認為“該市![]() 作物的種植點是否絕收與所在地域有關”?
作物的種植點是否絕收與所在地域有關”?
(3)根據(2)的結論,能否提供更好的調查方法來估計該市![]() 作物的種植點中,絕收種植點的比例?請說明理由.
作物的種植點中,絕收種植點的比例?請說明理由.


查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校有高三文科學生1000人,統計其高三上期期中考試的數學成績,得到頻率分布直方圖如下:
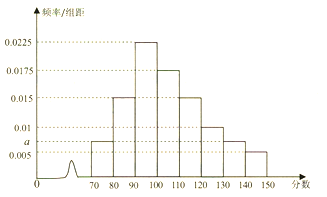
(1)求出圖中![]() 的值,并估計本次考試低于120分的人數;
的值,并估計本次考試低于120分的人數;
(2)假設同組的每個數據可用該組區間的中點值代替,試估計本次考試不低于120分的同學的平均數(其結果保留一位小數).
查看答案和解析>>
科目:高中數學 來源: 題型:
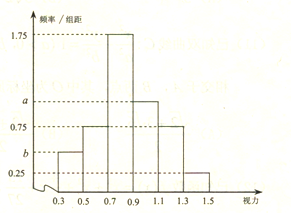
【題目】從某校高三年級中隨機抽取100名學生,對其高校招生體檢表中的視圖情況進行統計,得到如圖所示的頻率分布直方圖,已知從這100人中隨機抽取1人,其視力在![]() 的概率為
的概率為![]() .
.
(1)求![]() 的值;
的值;
(2)若某大學![]() 專業的報考要求之一是視力在0.9以上,則對這100人中能報考
專業的報考要求之一是視力在0.9以上,則對這100人中能報考![]() 專業的學生采用按視力分層抽樣的方法抽取8人,調查他們對
專業的學生采用按視力分層抽樣的方法抽取8人,調查他們對![]() 專業的了解程度,現從這8人中隨機抽取3人進行是否有意向報考該大學
專業的了解程度,現從這8人中隨機抽取3人進行是否有意向報考該大學![]() 專業的調查,記抽到的學生中視力在
專業的調查,記抽到的學生中視力在![]() 的人數為
的人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com