【題目】如圖所示，在正方體ABCDA1B1C1D1中，設線段A1C與平面ABC1D1交于點Q，求證：B，Q，D1三點共線．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】某校有高三文科學生1000人，統計其高三上期期中考試的數學成績，得到頻率分布直方圖如下：
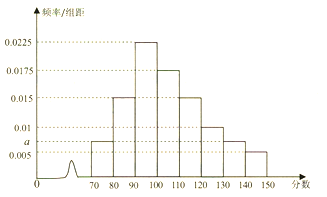
（1）求出圖中
的值，并估計本次考試低于120分的人數；
（2）假設同組的每個數據可用該組區間的中點值代替，試估計本次考試不低于120分的同學的平均數（其結果保留一位小數）.
查看答案和解析>>
科目：高中數學 來源： 題型：
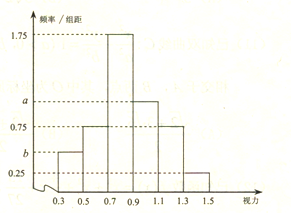
【題目】從某校高三年級中隨機抽取100名學生，對其高校招生體檢表中的視圖情況進行統計，得到如圖所示的頻率分布直方圖，已知從這100人中隨機抽取1人，其視力在
的概率為
.
（1）求
的值；
（2）若某大學
專業的報考要求之一是視力在0.9以上，則對這100人中能報考專業的學生采用按視力分層抽樣的方法抽取8人，調查他們對專業的了解程度，現從這8人中隨機抽取3人進行是否有意向報考該大學專業的調查，記抽到的學生中視力在
的人數為
，求的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出以下命題：
①雙曲線
的漸近線方程為y＝±
x；
②命題p：“x∈R，sinx＋
≥2”是真命題；
③已知線性回歸方程為
＝3＋2x，當變量x增加2個單位，其預報值平均增加4個單位；
④設隨機變量ξ服從正態分布N(0,1)，若P(ξ>1)＝0.2，則P(－1<ξ<0)＝0.6；
⑤設
，則
則正確命題的序號為________(寫出所有正確命題的序號)．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著經濟模式的改變，微商和電商已成為當今城鄉一種新型的購銷平臺．已知經銷某種商品的電商在任何一個銷售季度內，沒售出1噸該商品可獲利潤0.5萬元，未售出的商品，每1噸虧損0.3萬元．根據往年的銷售經驗，得到一個銷售季度內市場需求量的頻率分布直方圖如圖所示．已知電商為下一個銷售季度籌備了130噸該商品，現以
（單位：噸，
）表示下一個銷售季度的市場需求量，
（單位：萬元）表示該電商下一個銷售季度內經銷該商品獲得的利潤．
（Ⅰ）視分布在各區間內的頻率為相應的概率，求
；
（Ⅱ）將表示為的函數，求出該函數表達式；
（Ⅲ）在頻率分布直方圖的市場需求量分組中，以各組的區間中點值（組中值）代表該組的各個值，并以市場需求量落入該區間的頻率作為市場需求量取該組中值的概率（例如
，則取
的概率等于市場需求量落入
的頻率），求的分布列及數學期望
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某品牌汽車的
店，對最近100份分期付款購車情況進行統計，統計情況如下表所示.已知分9期付款的頻率為0.4；該店經銷一輛該品牌汽車，若顧客分3期付款，其利潤為1萬元；分6期或9期付款，其利潤為2萬元；分12期付款，其利潤為3萬元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
頻數 | 20 | 20 |
|
|
（1）若以上表計算出的頻率近似替代概率，從該店采用分期付款購車的顧客（數量較大）中隨機抽取3為顧客，求事件
：“至多有1位采用分6期付款“的概率
；
（2）按分層抽樣方式從這100為顧客中抽取5人，再從抽取的5人中隨機抽取3人，記該店在這3人身上賺取的總利潤為隨機變量
，求
的分布列和數學期望
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設圓
的圓心為A，直線
過點B（1,0）且與
軸不重合，交圓A于C，D兩點，過B作AC的平行線交AD于點E.
（Ⅰ）證明：
為定值，并寫出點E的軌跡方程；
（Ⅱ）設點E的軌跡為曲線C1，直線交C1于M,N兩點，過B且與垂直的直線與C1交于P,Q兩點， 求證：
是定值，并求出該定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
