
【題目】已知函數(shù)![]() .
.
(Ⅰ)當![]() 時,求
時,求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)設(shè)函數(shù)![]() 在點
在點![]() 處的切線為
處的切線為![]() ,直線
,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() .若點
.若點![]() 的縱坐標恒小于1,求實數(shù)
的縱坐標恒小于1,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為![]() ,單調(diào)遞增區(qū)間為
,單調(diào)遞增區(qū)間為![]() (Ⅱ)
(Ⅱ)![]()
【解析】試題分析:(Ⅰ)先明確函數(shù)定義域,再求函數(shù)導數(shù)![]() ,根據(jù)導函數(shù)零點進行分類討論:當
,根據(jù)導函數(shù)零點進行分類討論:當![]() 時,
時, ![]() ,因此減區(qū)間為
,因此減區(qū)間為![]() ,當
,當![]() 時,
時, ![]() 遞增區(qū)間為
遞增區(qū)間為![]() ,遞減區(qū)間為
,遞減區(qū)間為![]() (Ⅱ)根據(jù)導數(shù)幾何意義得切線的斜率
(Ⅱ)根據(jù)導數(shù)幾何意義得切線的斜率![]() ,再根據(jù)點斜式寫出切線方程
,再根據(jù)點斜式寫出切線方程![]() ,得點
,得點![]() 的縱坐標
的縱坐標![]() ,即不等式
,即不等式![]() 恒成立,而不等式恒成立問題,一般轉(zhuǎn)化為對應(yīng)函數(shù)最值問題::
恒成立,而不等式恒成立問題,一般轉(zhuǎn)化為對應(yīng)函數(shù)最值問題:: ![]() 的最大值,利用導數(shù)研究函數(shù)
的最大值,利用導數(shù)研究函數(shù)![]() 單調(diào)性,為單調(diào)遞減,再利用洛必達法則得
單調(diào)性,為單調(diào)遞減,再利用洛必達法則得![]() ,因此
,因此![]() ,也可直接構(gòu)造差函數(shù),分類討論最值進行求解
,也可直接構(gòu)造差函數(shù),分類討論最值進行求解
試題解析:解:(1)當![]() 時,
時, ![]() .……………………1分
.……………………1分
所以,當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .………………3分
.………………3分
所以函數(shù)![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為![]() ,單調(diào)遞增區(qū)間為
,單調(diào)遞增區(qū)間為![]() .……………………4分
.……………………4分
(2)因為![]() ,所以
,所以![]() 處切線的斜率
處切線的斜率![]() ,
,
所以切線![]() 的方程為
的方程為![]() ,
,
令![]() 得,
得, ![]() .………………………………5分
.………………………………5分
當![]() 時,要使得點
時,要使得點![]() 的縱坐標恒小于1,
的縱坐標恒小于1,
只需![]() ,即
,即![]() .…………………………6分
.…………………………6分
令![]() ,則
,則![]() .………………………………7分
.………………………………7分
因為![]() ,所以
,所以![]() ,
,
①若![]() ,即
,即![]() 時,
時, ![]() ,
,
所以,當![]() 時,
時, ![]() ,即
,即![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
所以![]() 恒成立,所以
恒成立,所以![]() 滿足題意.………………………………8分
滿足題意.………………………………8分
②若![]() 即
即![]() 時,
時, ![]() ,
,
所以,當![]() 時,
時, ![]() ,即
,即![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
所以![]() ,所以
,所以![]() 不滿足題意.…………………………9分
不滿足題意.…………………………9分
③若![]() ,即
,即![]() 時,
時, ![]() ,
,
則![]() 、
、![]() 、
、![]() 的關(guān)系如下表:
的關(guān)系如下表:
|
|
|
|
|
| 0 |
|
| 遞減 | 極小值 | 遞增 |
所以![]() ,所以
,所以![]() 不滿足題意,
不滿足題意,
結(jié)合①②③,可得,當![]() 時,
時, ![]() 時,此時點
時,此時點![]() 的縱坐標恒小于1.………………12分
的縱坐標恒小于1.………………12分


科目:高中數(shù)學 來源: 題型:
【題目】規(guī)定:投擲飛鏢3次為一輪,若3次中至少兩次投中8環(huán)以上為優(yōu)秀.根據(jù)以往經(jīng)驗某選手投擲一次命中8環(huán)以上的概率為![]() .現(xiàn)采用計算機做模擬實驗來估計該選手獲得優(yōu)秀的概率: 用計算機產(chǎn)生0到9之間的隨機整數(shù),用0,1表示該次投擲未在 8 環(huán)以上,用2,3,4,5,6,7,8,9表示該次投擲在 8 環(huán)以上,經(jīng)隨機模擬試驗產(chǎn)生了如下 20 組隨機數(shù):
.現(xiàn)采用計算機做模擬實驗來估計該選手獲得優(yōu)秀的概率: 用計算機產(chǎn)生0到9之間的隨機整數(shù),用0,1表示該次投擲未在 8 環(huán)以上,用2,3,4,5,6,7,8,9表示該次投擲在 8 環(huán)以上,經(jīng)隨機模擬試驗產(chǎn)生了如下 20 組隨機數(shù):
907 966 191 925 271 932 812 458 569 683
031 257 393 527 556 488 730 113 537 989
據(jù)此估計,該選手投擲 1 輪,可以拿到優(yōu)秀的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知y=ax2+bx(a<0)通過點(1,2),且其圖象與y=﹣x2+2x的圖象有二個交點(如圖所示). 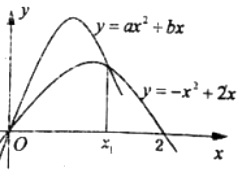
(1)求y=ax2+bx與y=﹣x2+2x所圍成的面積S與a的函數(shù)關(guān)系;
(2)當a,b為何值時,S取得最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值;
上的最大值;
(2)若![]() 是函數(shù)
是函數(shù)![]() 圖像上不同的三點,且
圖像上不同的三點,且![]() ,試判斷
,試判斷![]() 與
與![]() 之間的大小關(guān)系,并證明.
之間的大小關(guān)系,并證明.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)y=f(x)的定義域為D,若對于任意x1、x2∈D,當x1+x2=2a時,恒有f(x1)+f(x2)=2b,則稱點(a,b)為函數(shù)y=f(x)圖象的對稱中心.研究函數(shù)f(x)=x+sinπx﹣3的某一個對稱中心,并利用對稱中心的上述定義,可得到f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(
)+f( ![]() )的值為( )
)的值為( )
A.4027
B.﹣4027
C.8054
D.﹣8054
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)f(x)在定義域[﹣1,1]是奇函數(shù),當x∈[﹣1,0]時,f(x)=﹣3x2 .
(1)當x∈[0,1],求f(x);
(2)對任意a∈[﹣1,1],x∈[﹣1,1],不等式f(x)≤2cos2θ﹣asinθ+1都成立,求θ的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() .
.
(Ⅰ)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若曲線![]() 在點
在點![]() 處的切線
處的切線![]() 與曲線
與曲線![]() 切于點
切于點![]() ,求
,求![]() 的值;
的值;
(Ⅲ)若![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】【選做題】在A、B、C、D四小題中只能選做2題,每小題10分,共計20分.請在答卷卡指定區(qū)域內(nèi)作答.解答應(yīng)寫出文字說明、證明過程或演算步驟.
A.選修4—1:幾何證明選講
如圖,△ABC的頂點A,C在圓O上,B在圓外,線段AB與圓O交于點M.

(1)若BC是圓O的切線,且AB=8,BC=4,求線段AM的長度;
(2)若線段BC與圓O交于另一點N,且AB=2AC,求證:BN=2MN.
B.選修4—2:矩陣與變換
設(shè)a,b∈R.若直線l:ax+y-7=0在矩陣A= ![]() 對應(yīng)的變換作用下,得到的直線為l′:9x+y-91=0.求實數(shù)a,b的值.
對應(yīng)的變換作用下,得到的直線為l′:9x+y-91=0.求實數(shù)a,b的值.
C.選修4—4:坐標系與參數(shù)方程
在平面直角坐標系xOy中,直線l:  (t為參數(shù)),與曲線C:
(t為參數(shù)),與曲線C:  (k為參數(shù))交于A,B兩點,求線段AB的長.
(k為參數(shù))交于A,B兩點,求線段AB的長.
D.選修4—5:不等式選講
設(shè)a≠b,求證:a4+6a2b2+b4>4ab(a2+b2).
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com