【題目】已知直線
，拋物線C：
上一動點P到直線
和
軸距離之和的最小值是（ ）
A.1B.2C.
D.
【答案】A
【解析】
拋物線
上一動點P到直線
和
軸距離之和最小轉化為：拋物線上一動點P到直線和直線x＝-1的距離之和最小，x＝1是拋物線的準線，則P到x＝1的距離等于PF，F（1，0）為拋物線的焦點，過F作
垂線，和拋物線的交點就是P，所以點P到直線
的距離和到軸的距離之和的最小值就是F（1，0）到直線距離再減1．
解：x＝1是拋物線的準線，拋物線的焦點F（1，0），
則P到x＝1的距離等于PF，
過F作垂線，和拋物線的交點就是P，
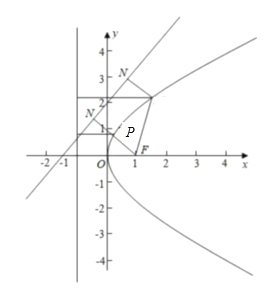
所以點P到直線：的距離和到直線：x＝1的距離之和的最小值
就是F（1，0）到直線距離，
所以最小值
．
拋物線上一動點P到直線和軸的距離之和的最小值是：21＝1
故選：A．
科目：高中數學 來源： 題型：
【題目】平面直角坐標系中，
為坐標原點，射線
與
軸正半軸重合，射線
在第一象限，且與軸正半軸的夾角為
，在上有點列
，在上有點
，已知
，
（1）求點
和
的坐標；
（2）求
的坐標；
（3）求
面積的最大值，并求出此時的
值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C：
，直線1過原點O．
（1）若直線l與圓C相切，求直線l的斜率；
（2）若直線l與圓C交于A、B兩點，點P的坐標為
，若
．求直線l的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠去年某產品的年產量為100萬只，每只產品的銷售價為10元，固定成本為8元
今年，工廠第一次投入100萬元
科技成本
，并計劃以后每年比上一年多投入100萬元科技成本，預計產量年遞增10萬只，第
次投入后，每只產品的固定成本為
為常數，
且
，若產品銷售價保持不變，第次投入后的年利潤為
萬元．
（1）求
的值，并求出的表達式；
（2）問從今年算起第幾年利潤最高？最高利潤為多少萬元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題正確的是
（1）命題“
，
”的否定是“
，
”；
（2）l為直線，
，
為兩個不同的平面，若
，
，則
；
（3）給定命題p，q，若“
為真命題”，則
是假命題；
（4）“
”是“
”的充分不必要條件．
A. （1）（4）B. （2）（3）C. （3）（4）D. （1）（3）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
