
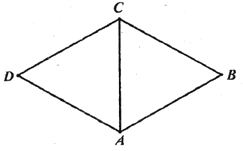
【題目】![]() 分別為菱形
分別為菱形![]() 的邊
的邊![]() 的中點,將菱形沿對角線
的中點,將菱形沿對角線![]() 折起,使點
折起,使點![]() 不在平面
不在平面![]() 內,則在翻折過程中,以下命題正確的是___________.(寫出所有正確命題的序號)
內,則在翻折過程中,以下命題正確的是___________.(寫出所有正確命題的序號)
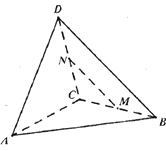
①![]() 平面
平面![]() ;②異面直線
;②異面直線![]() 與
與![]() 所成的角為定值;③在二面角
所成的角為定值;③在二面角![]() 逐漸漸變小的過程中,三棱錐
逐漸漸變小的過程中,三棱錐![]() 的外接球半徑先變小后變大;④若存在某個位程,使得直線
的外接球半徑先變小后變大;④若存在某個位程,使得直線![]() 與直線
與直線![]() 垂直,則
垂直,則![]() 的取值范圍是
的取值范圍是![]() .
.
【答案】①②④
【解析】
①由![]() ,可得證;②取AC中點P,可證得
,可得證;②取AC中點P,可證得![]() 平面DPB,可得正;③ 借助極限狀態,當平面DCA與平面BCA重合時,三棱錐
平面DPB,可得正;③ 借助極限狀態,當平面DCA與平面BCA重合時,三棱錐![]() 的外接球即為以三角形ABC的外接圓為圓心,半徑為半徑的球,二面角不為0時,外接圓的半徑一定大于此半徑,不正確. ④
的外接球即為以三角形ABC的外接圓為圓心,半徑為半徑的球,二面角不為0時,外接圓的半徑一定大于此半徑,不正確. ④
過A在平面ABC中作![]() 交BC于H,分析H點在BC上的位置,可得證.
交BC于H,分析H點在BC上的位置,可得證.
①由![]() 分別為菱形
分別為菱形![]() 的邊
的邊![]() 的中點,故
的中點,故![]() ,
,![]() 平面ABD,故
平面ABD,故![]() 平面
平面![]() ;
;
②取AC中點P,連接DP,BP,由于菱形ABCD,所以![]() ,可證得
,可證得![]() 平面DPB,故
平面DPB,故![]() ,又
,又![]() ,故
,故![]() ,異面直線
,異面直線![]() 與
與![]() 所成的角為定值.
所成的角為定值.

③ 借助極限狀態,當平面DCA與平面BCA重合時,三棱錐![]() 的外接球即為以三角形ABC的外接圓為圓心,半徑為半徑的球,當二面角變大時球心離開平面ABC,但球心在平面ABC的投影仍然為三角形ABC的外接圓的圓心,故二面角不為0時,外接球半徑一定大于三角形ABC的外接圓半徑,故三棱錐
的外接球即為以三角形ABC的外接圓為圓心,半徑為半徑的球,當二面角變大時球心離開平面ABC,但球心在平面ABC的投影仍然為三角形ABC的外接圓的圓心,故二面角不為0時,外接球半徑一定大于三角形ABC的外接圓半徑,故三棱錐![]() 的外接球半徑不可能先變小后變大.
的外接球半徑不可能先變小后變大.
④
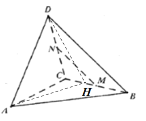
過A在平面ABC中作![]() 交BC于H,若
交BC于H,若![]() 為銳角,H在線段BC上;若
為銳角,H在線段BC上;若![]() 為直角,H與B點重合;
為直角,H與B點重合;![]() 為鈍角,H在線段BC的延長線射線CB上.
為鈍角,H在線段BC的延長線射線CB上.
若存在某個位程,使得直線![]() 與直線
與直線![]() 垂直,由于
垂直,由于![]() ,因此
,因此![]() 平面AHD,
平面AHD,
故![]() .
.
若![]() 為直角,H與B點重合,即
為直角,H與B點重合,即![]() ,由于
,由于![]() ,不可能成立.
,不可能成立.
若![]() 為鈍角,則原平面圖中,
為鈍角,則原平面圖中,![]() 為銳角,由于立體圖中
為銳角,由于立體圖中![]() ,故立體圖中
,故立體圖中![]() 一定比原圖中更小,因此
一定比原圖中更小,因此![]() 為銳角,
為銳角,![]() ,故H在線段CB上,與H在線段BC的延長線射線CB上矛盾,因此
,故H在線段CB上,與H在線段BC的延長線射線CB上矛盾,因此![]() 的取值范圍是
的取值范圍是![]() .
.
故答案為:①②④


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中數學 來源: 題型:
【題目】京劇是我國的國粹,是“國家級非物質文化遺產”,為紀念著名京劇表演藝術家,京劇藝術大師梅蘭芳先生,某電視臺《我愛京劇》的一期比賽中,2位“梅派”傳人和4位京劇票友(資深業余愛好者)在幕后登臺演唱同一曲目《貴妃醉酒》選段,假設6位演員的演唱水平相當,由現場40位大眾評委和“梅派”傳人的朋友猜測哪兩位是真正的“梅派”傳人.
(1)此欄目編導對本期的40位大眾評委的年齡和對京劇知識的了解進行調查,根據調查得到的數據如下:
京劇票友 | 一般愛好者 | 合計 | |
50歲以上 | 15 | 10 | 25 |
50歲以下 | 3 | 12 | 15 |
合計 | 18 | 22 | 40 |
試問:在犯錯誤的概率不超過多少的前提下,可以認為年齡的大小與對京劇知識的了解有關系?
(2)若在一輪中演唱中,每猜出一位亮相一位,且規定猜出2位“梅派”傳人”或猜出5人后就終止,記本輪競猜一共競猜![]() 次,求隨機變量
次,求隨機變量![]() 的分布列與期望.
的分布列與期望.
參考數據:
0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓C:
中,橢圓C:![]() (
(![]() )的左、右焦點分別為
)的左、右焦點分別為![]() ,
,![]() ,直線l:
,直線l:![]() 交橢圓C于A,B兩點,且
交橢圓C于A,B兩點,且![]() 的周長為8.
的周長為8.
(1)求橢圓C的方程;
(2)若線段![]() 的中點為P,直線
的中點為P,直線![]() 與橢圓C交于M,N兩點,且
與橢圓C交于M,N兩點,且![]() ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在梯形ABCD中,AD∥BC,AB=BC![]() 2,E為AD的中點,O是AC與BE的交點,將△ABE沿BE翻折到圖2中△A1BE的位置得到四棱錐A1﹣BCDE.
2,E為AD的中點,O是AC與BE的交點,將△ABE沿BE翻折到圖2中△A1BE的位置得到四棱錐A1﹣BCDE.
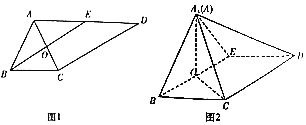
(1)求證:CD⊥A1C;
(2)若A1C![]() ,BE=2
,BE=2![]() ,求點C到平面A1ED的距離.
,求點C到平面A1ED的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓C:
中,已知橢圓C:![]() (
(![]() >
>![]() >0)的右焦點為F(1,0),且過點(1,
>0)的右焦點為F(1,0),且過點(1,![]() ),過點F且不與
),過點F且不與![]() 軸重合的直線
軸重合的直線![]() 與橢圓C交于A,B兩點,點P在橢圓上,且滿足
與橢圓C交于A,B兩點,點P在橢圓上,且滿足![]() .
.
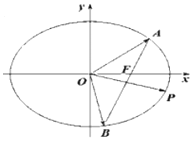
(1)求橢圓C的標準方程;
(2)若![]() ,求直線AB的方程.
,求直線AB的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() .
.
(1)若![]() ,判斷函數
,判斷函數![]() 是否存在極值,若存在,求出極值:若不存在,說明理由:
是否存在極值,若存在,求出極值:若不存在,說明理由:
(2)若![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍:
的取值范圍:
(3)若函數![]() 存在兩個極值點
存在兩個極值點![]() ,證明:
,證明:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正三棱柱(底面為正三角形的直棱柱)ABC﹣A1B1C1中,已知AB=AA1=2,點Q為BC的中點.
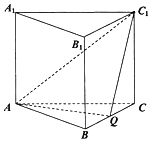
(1)求證:平面AQC1⊥平面B1BCC1;
(2)求直線CC1與平面AQC1所成角的正切值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com