
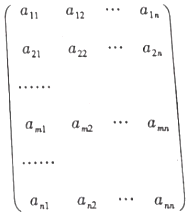
【題目】在如圖所示的數(shù)陣中每一行從左到右均是首項(xiàng)為1,項(xiàng)數(shù)為n的等差數(shù)列,設(shè)第![]() 行的等差數(shù)列中的第k項(xiàng)為
行的等差數(shù)列中的第k項(xiàng)為![]() 2,3,
2,3,![]() ,
,![]() ,公差為
,公差為![]() ,若
,若![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 也成等差數(shù)列.
也成等差數(shù)列.
![]() Ⅰ
Ⅰ![]() 求
求![]() ;
;
![]() Ⅱ
Ⅱ![]() 求
求![]() 關(guān)于m的表達(dá)式;
關(guān)于m的表達(dá)式;
![]() Ⅲ
Ⅲ![]() 若數(shù)陣中第i行所有數(shù)之和
若數(shù)陣中第i行所有數(shù)之和![]() ,第j列所有數(shù)之和為
,第j列所有數(shù)之和為![]() ,是否存在i,j滿(mǎn)足
,是否存在i,j滿(mǎn)足![]() ,使得
,使得![]() 成立?若存在,請(qǐng)求出i,j的一組值;若不存在,請(qǐng)說(shuō)明理由.
成立?若存在,請(qǐng)求出i,j的一組值;若不存在,請(qǐng)說(shuō)明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
,![]() 其中
其中![]() ;(Ⅲ)不存在.
;(Ⅲ)不存在.
【解析】
本題的數(shù)陣中蘊(yùn)涵著很多個(gè)等差數(shù)列,包括每一行都成等差數(shù)列,最后一列也成等差數(shù)列,每一行的公差也成等差數(shù)列,把握住這些,然后細(xì)心運(yùn)算.
解:![]() Ⅰ
Ⅰ![]() 由題意,可知:
由題意,可知:
![]() 數(shù)陣中的第1行是以
數(shù)陣中的第1行是以![]() 為首項(xiàng),
為首項(xiàng),![]() 為公差的等差數(shù)列,
為公差的等差數(shù)列,
![]() 數(shù)陣中的第1行的最后一項(xiàng)
數(shù)陣中的第1行的最后一項(xiàng)![]() .
.
又![]() 數(shù)陣中的第2行是以
數(shù)陣中的第2行是以![]() 為首項(xiàng),
為首項(xiàng),![]() 為公差的等差數(shù)列,
為公差的等差數(shù)列,
![]() 數(shù)陣中的第2行的最后一項(xiàng)
數(shù)陣中的第2行的最后一項(xiàng)![]() .
.
![]() 數(shù)陣中的每行的最后一項(xiàng)
數(shù)陣中的每行的最后一項(xiàng)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 也成等差數(shù)列.
也成等差數(shù)列.
![]() .
.
![]() Ⅱ
Ⅱ![]() 由
由![]() Ⅰ
Ⅰ![]() 可知:
可知:
![]() ,
,![]() .
.
數(shù)陣中的每行的最后一項(xiàng)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是以
是以![]() 為首項(xiàng),
為首項(xiàng),![]() 為公差的等差數(shù)列.
為公差的等差數(shù)列.
![]() 等差數(shù)列
等差數(shù)列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 中的第m項(xiàng)
中的第m項(xiàng)![]() .
.
![]() 數(shù)陣第m行中第1項(xiàng)
數(shù)陣第m行中第1項(xiàng)![]() ,最后一項(xiàng)第n項(xiàng)
,最后一項(xiàng)第n項(xiàng)![]() ,而數(shù)陣第m行也是等差數(shù)列.
,而數(shù)陣第m行也是等差數(shù)列.
![]() 數(shù)陣第m行的公差
數(shù)陣第m行的公差![]() .
.
![]() ,
,![]() 其中
其中![]() .
.
![]() Ⅲ
Ⅲ![]() 由題意及
由題意及![]() Ⅰ
Ⅰ![]() Ⅱ
Ⅱ![]() ,可知:
,可知:
數(shù)陣中第i行是以![]() 為首項(xiàng),
為首項(xiàng),![]() 為公差的等差數(shù)列.
為公差的等差數(shù)列.
![]() .
.
由![]() Ⅱ
Ⅱ![]() 可知:
可知:
![]() 是以1為首項(xiàng),2為公差的等差數(shù)列.
是以1為首項(xiàng),2為公差的等差數(shù)列.
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
等差數(shù)列![]() .
.
假設(shè)![]() 成立,即
成立,即![]() .
.
整理,得:![]()
要使此式成立,必須有:
![]() ,
,
解得:![]() ,
,![]() 很明顯,這與題中條件
很明顯,這與題中條件![]() 相矛盾.
相矛盾.
![]() 不存在i,j的一組值,使得
不存在i,j的一組值,使得![]() 成立.
成立.


 津橋教育計(jì)算小狀元系列答案
津橋教育計(jì)算小狀元系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=![]() ,若x1,x2∈R,且x1≠x2,使得f(x1)=f(x2),則實(shí)數(shù)a的取值范圍是( )
,若x1,x2∈R,且x1≠x2,使得f(x1)=f(x2),則實(shí)數(shù)a的取值范圍是( )
A. [2,3]∪(﹣∞,﹣5]B. (﹣∞,2)∪(3,5)
C. [2,3]D. [5,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
![]() 當(dāng)
當(dāng)![]() 時(shí),
時(shí),![]() ,求實(shí)數(shù)a的取值范圍;
,求實(shí)數(shù)a的取值范圍;
![]() 當(dāng)
當(dāng)![]() 時(shí),曲線
時(shí),曲線![]() 和曲線
和曲線![]() 是否存在公共切線?并說(shuō)明理由.
是否存在公共切線?并說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在多面體![]() 中,四邊形
中,四邊形![]() 為正方形,
為正方形,![]() ,
,![]() ,
,![]() .
.
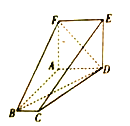
(1)證明:平面![]() 平面
平面![]() .
.
(2)若![]() 平面
平面![]() ,二面角
,二面角![]() 為
為![]() ,三棱錐
,三棱錐![]() 的外接球的球心為
的外接球的球心為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了解某品種一批樹(shù)苗生長(zhǎng)情況,在該批樹(shù)苗中隨機(jī)抽取了容量為120的樣本,測(cè)量樹(shù)苗高度(單位:cm),經(jīng)統(tǒng)計(jì),其高度均在區(qū)間[19,31]內(nèi),將其按[19,21),[21,23),[23,25),[25,27),[27,29),[29,31]分成6組,制成如圖所示的頻率分布直方圖.其中高度為27 cm及以上的樹(shù)苗為優(yōu)質(zhì)樹(shù)苗.
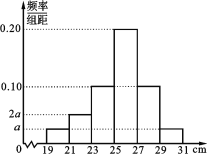
(1)求圖中a的值;
(2)已知所抽取的這120棵樹(shù)苗來(lái)自于A,B兩個(gè)試驗(yàn)區(qū),部分?jǐn)?shù)據(jù)如下列聯(lián)表:
A試驗(yàn)區(qū) | B試驗(yàn)區(qū) | 合計(jì) | |
優(yōu)質(zhì)樹(shù)苗 | 20 | ||
非優(yōu)質(zhì)樹(shù)苗 | 60 | ||
合計(jì) |
將列聯(lián)表補(bǔ)充完整,并判斷是否有99.9%的把握認(rèn)為優(yōu)質(zhì)樹(shù)苗與A,B兩個(gè)試驗(yàn)區(qū)有關(guān)系,并說(shuō)明理由;
(3)用樣本估計(jì)總體,若從這批樹(shù)苗中隨機(jī)抽取4棵,其中優(yōu)質(zhì)樹(shù)苗的棵數(shù)為X,求X的分布列和數(shù)學(xué)期望EX.
下面的臨界值表僅供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:![]() ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,四棱錐![]() 的底面
的底面![]() 是矩形,側(cè)面
是矩形,側(cè)面![]() 是正三角形,
是正三角形,![]() ,
,![]() ,
,![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 為
為![]() 中點(diǎn),求二面角
中點(diǎn),求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在多面體![]() 中,四邊形
中,四邊形![]() 是菱形,
是菱形,![]() ,四邊形
,四邊形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() .
.
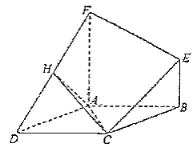
(Ⅰ)證明:![]() 平面
平面![]() .
.
(Ⅱ)若平面![]() 平面
平面![]() ,
,![]() 為
為![]() 的中點(diǎn),求平面
的中點(diǎn),求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】
某位同學(xué)進(jìn)行寒假社會(huì)實(shí)踐活動(dòng),為了對(duì)白天平均氣溫與某奶茶店的某種飲料銷(xiāo)量之間的關(guān)系進(jìn)行分析研究,他分別記錄了1月11日至1月15日的白天平均氣溫![]() (°C)與該奶茶店的這種飲料銷(xiāo)量
(°C)與該奶茶店的這種飲料銷(xiāo)量![]() (杯),得到如下數(shù)據(jù):
(杯),得到如下數(shù)據(jù):
日 期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均氣溫 | 9 | 10 | 12 | 11 | 8 |
銷(xiāo)量 | 23 | 25 | 30 | 26 | 21 |
(1)若從這五組數(shù)據(jù)中隨機(jī)抽出2組,求抽出的2組數(shù)據(jù)恰好是相鄰2天數(shù)據(jù)的概率;
(2)請(qǐng)根據(jù)所給五組數(shù)據(jù),求出y關(guān)于x的線性回歸方程![]() .
.
(參考公式: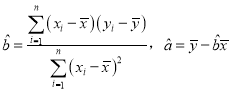 .)
.)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2018年10月28日,重慶公交車(chē)墜江事件震驚全國(guó),也引發(fā)了廣大群眾的思考——如何做一個(gè)文明的乘客.全國(guó)各地大部分社區(qū)組織居民學(xué)習(xí)了文明乘車(chē)規(guī)范.![]() 社區(qū)委員會(huì)針對(duì)居民的學(xué)習(xí)結(jié)果進(jìn)行了相關(guān)的問(wèn)卷調(diào)查,并將得到的分?jǐn)?shù)整理成如圖所示的統(tǒng)計(jì)圖.
社區(qū)委員會(huì)針對(duì)居民的學(xué)習(xí)結(jié)果進(jìn)行了相關(guān)的問(wèn)卷調(diào)查,并將得到的分?jǐn)?shù)整理成如圖所示的統(tǒng)計(jì)圖.

(Ⅰ)求得分在![]() 上的頻率;
上的頻率;
(Ⅱ)求![]() 社區(qū)居民問(wèn)卷調(diào)查的平均得分的估計(jì)值;(同一組中的數(shù)據(jù)以這組數(shù)據(jù)所在區(qū)間中點(diǎn)的值作代表)
社區(qū)居民問(wèn)卷調(diào)查的平均得分的估計(jì)值;(同一組中的數(shù)據(jù)以這組數(shù)據(jù)所在區(qū)間中點(diǎn)的值作代表)
(Ⅲ)以頻率估計(jì)概率,若在全部參與學(xué)習(xí)的居民中隨機(jī)抽取5人參加問(wèn)卷調(diào)查,記得分在![]() 間的人數(shù)為
間的人數(shù)為![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com