【題目】計算下列各式的值，寫出必要的計算過程．
（1）0.064 
﹣（﹣ 
）0+16 
+0.25 
（2）（log43+log83）（log32+log92）
【答案】
（1）解：0.064 
﹣（﹣ 
）0+16 
+0.25 
=[（0.4）3] ﹣1+（24） +（0.52）
=0.4﹣1﹣1+23+0.5
= 
﹣1+8+0.5
=10
（2）解：（log43+log83）（log32+log92）
=（log6427+log649）（log94+log92）
=log64243log98
= 
= 
= 
【解析】（1）利用有理數(shù)指數(shù)冪的性質(zhì)、運算法則求解．（2）利用對數(shù)的性質(zhì)、換底公式、運算法則求解．
【考點精析】根據(jù)題目的已知條件，利用對數(shù)的運算性質(zhì)的相關(guān)知識可以得到問題的答案，需要掌握①加法：
②減法：
③數(shù)乘：
④
⑤
．
名校提分一卷通系列答案
課程達標(biāo)測試卷闖關(guān)100分系列答案
新卷王期末沖刺100分系列答案
全能闖關(guān)100分系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知集合A={x|x2﹣5x﹣6＜0}，集合B={x|6x2﹣5x+1≥0}，集合C={x|（x﹣m）（x﹣m﹣9）＜0}
（1）求A∩B；
（2）若AC，求實數(shù) m的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知圓O的方程為x2+y2=1，直線l1過點A（3，0），且與圓O相切．
（1）求直線l1的方程；
（2）設(shè)圓O與x軸相交于P，Q兩點，M是圓O上異于P，Q的任意一點，過點A且與x軸垂直的直線為l2 ， 直線PM交直線l2于點P′，直線QM交直線l2于點Q′．求證：以P′Q′為直徑的圓C總經(jīng)過定點，并求出定點坐標(biāo)．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在三棱錐P﹣ABC中，PA⊥平面ABC，AC⊥BC，D為側(cè)棱PC的中點，它的正（主）視圖和側(cè)（左）視圖如圖所示．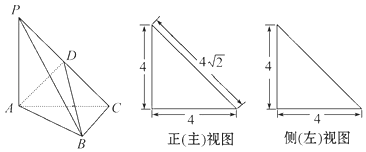 
（Ⅰ）求三棱錐P﹣ABD的體積．
（Ⅱ）在∠ACB的平分線所在直線上確定一點Q，使得PQ∥平面ABD，并求此時PQ的長．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】函數(shù)
.
（I）函數(shù)
在點
處的切線與直線
垂直，求a的值；
（II）討論函數(shù)
的單調(diào)性；
（III）不等式
在區(qū)間
上恒成立，求實數(shù)a的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知p：直線y=（2m+1）x+m﹣2的圖象不經(jīng)過第四象限，q：方程x2+ 
=1表示焦點在x軸上的橢圓，若（￢p）∨q為假命題，求實數(shù)m的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
,圓
的圓心
在橢圓
上，點
到橢圓的右焦點的距離為
.
（1）求橢圓的方程；
（2）過點
作互相垂直的兩條直線
,且
交橢圓
于
兩點, 直線
交圓
于
兩點, 且
為
的中點, 求
的面積的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知集合A={x|m+1≤x≤2m﹣1}，B={x|x＜﹣2或x＞5}
（1）若AB，求實數(shù)m的取值范圍的集合；
（2）若A∩B=，求實數(shù)m的取值范圍的集合．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
